《剑指Offer》对称的二叉树

题目描述：

  请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。

解题思路：

  我们通常有三种不同的二叉树遍历算法，即前序遍历、中序遍历和后序遍历。在这三种遍历算法中，都是先遍历左子结点再遍历右子结点。以前序遍历为例，我们可以定义一个遍历算法，先遍历右子结点再遍历左子结点，暂且称其为前序遍历的对称遍历。

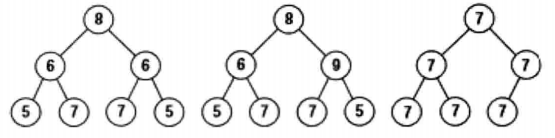
遍历第一棵树，前序遍历的遍历序列为{8,6,5,7,6,7,5}，其对称遍历的遍历序列为{8,6,5,7,6,7,5}。

遍历第二颗树，前序遍历的遍历序列为{8,6,5,7,9,7,5}，其对称遍历的遍历序列为{8,9,5,7,6,7,5}。

可以看到，使用此方法可以区分前两棵树，第一棵树为对称树，第二颗树不是对称树。但是当使用此方法，你会发现第三颗树的前序遍历和对称前序遍历的遍历序列是一样的。

怎么区分第三颗树呢？解决办法就是我们也要考虑NULL指针。此时，前序遍历的遍历序列{7,7,7,NULL,NULL,7,NULL,NULL,7,7,NLL,NULL,NULL}，其对称遍历的遍历序列为{7,7,NULL,7,NULL,NULL,7,7,NULL,NULL,7,NULL,NULL}。因为两种遍历的序列不同，因此这棵树不是对称树。

代码实现(c++)

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
public:
    bool isSymmetrical(TreeNode* pRoot)
    {
        if(pRoot == NULL){
            return true;
        }
        return isSymmetriacalCor(pRoot, pRoot);
    }
private:
    bool isSymmetriacalCor(TreeNode* pRoot1, TreeNode* pRoot2){
        if(pRoot1 == NULL && pRoot2 == NULL){
            return true;
        }
        if(pRoot1 == NULL || pRoot2 == NULL){
            return false;
        }
        if(pRoot1->val != pRoot2->val){
            return false;
        }
        return isSymmetriacalCor(pRoot1->left, pRoot2->right) && isSymmetriacalCor(pRoot1->right, pRoot2->left);
    }
};

代码实现(java)

public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }
}
public class Solution {
    boolean isSymmetrical(TreeNode pRoot) {
        return isSymmctrical(pRoot, pRoot);
    }

    public boolean isSymmctrical(TreeNode root1, TreeNode root2) {
        if(root1 == null && root2 == null) {
            return true;
        }
        if(root1 == null || root2 == null) {
            return false;
        }

        if(root1.val != root2.val) {
            return false;
        }

        return isSymmctrical(root1.left, root2.right) && isSymmctrical(root1.right, root2.left);
    }
}

代码实现(python)

Tree(self, left, right):
        if not left and not right:
            return True
        if not left or not right:
            return False
        if left.val == right.val:
            return self.recursiveTree(left.left, right.right) and self.recursiveTree(left.right, right.left)
        return False
if __name__=='__main__':

    A1 = TreeNode(1)
    A2 = TreeNode(2)
    A3 = TreeNode(2)
    A4 = TreeNode(3)
    A5 = TreeNode(4)
    A6 = TreeNode(4)
    A7 = TreeNode(3)

    A1.left=A2
    A1.right=A3
    A2.left=A4
    A2.right=A5
    A3.left=A6
    A3.right=A7


    solution = Solution()
    ans=solution.isSymmetrical(A1)
    print(ans)