《剑指Offer》树的子结构

题目描述：

  输入两棵二叉树A，B，判断B是不是A的子结构。（ps：我们约定空树不是任意一个树的子结构）

解题思路：

  要查找树A中是否存在和树B结构一样的子树，我们可以分为两步：第一步，在树A中找到和树B的根结点值一样的结点R；第二步，判断树A中以R为根结点的子树是不是包含和树B一样的结构。

  对于这两步，第一步实际上就是树的遍历，第二步是判断是否有相同的结构，这两步都可以通过递归来实现。

  举例：

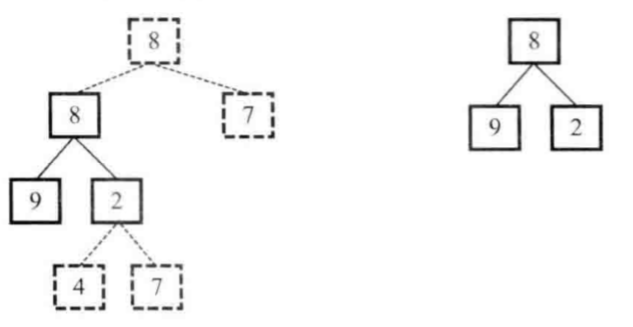
代码实现(c++)

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/
class Solution {
public:
    bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2)
    {
        bool result = false;
        if(pRoot1 != NULL && pRoot2 != NULL){
            if(pRoot1->val == pRoot2->val){
            result = DoesTree1HasTree2(pRoot1, pRoot2);
        }
            if(!result){
                result = HasSubtree(pRoot1->left, pRoot2);
            }
            if(!result){
                result = HasSubtree(pRoot1->right, pRoot2);
            }
        }
        return result;
    }
private:
    bool DoesTree1HasTree2(TreeNode* pRoot1, TreeNode* pRoot2){
        if(pRoot2 == NULL){
            return true;
        }
        if(pRoot1 == NULL){
            return false;
        }
        if(pRoot1->val != pRoot2->val){
            return false;
        }
        return DoesTree1HasTree2(pRoot1->left, pRoot2->left) && DoesTree1HasTree2(pRoot1->right, pRoot2->right);
    }
};