《剑指Offer》二叉树的下一个结点

题目描述：

  给定一个二叉树和其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的指针。

解题思路：

  首先要做的就是要知道二叉树的中序遍历。具体如下：

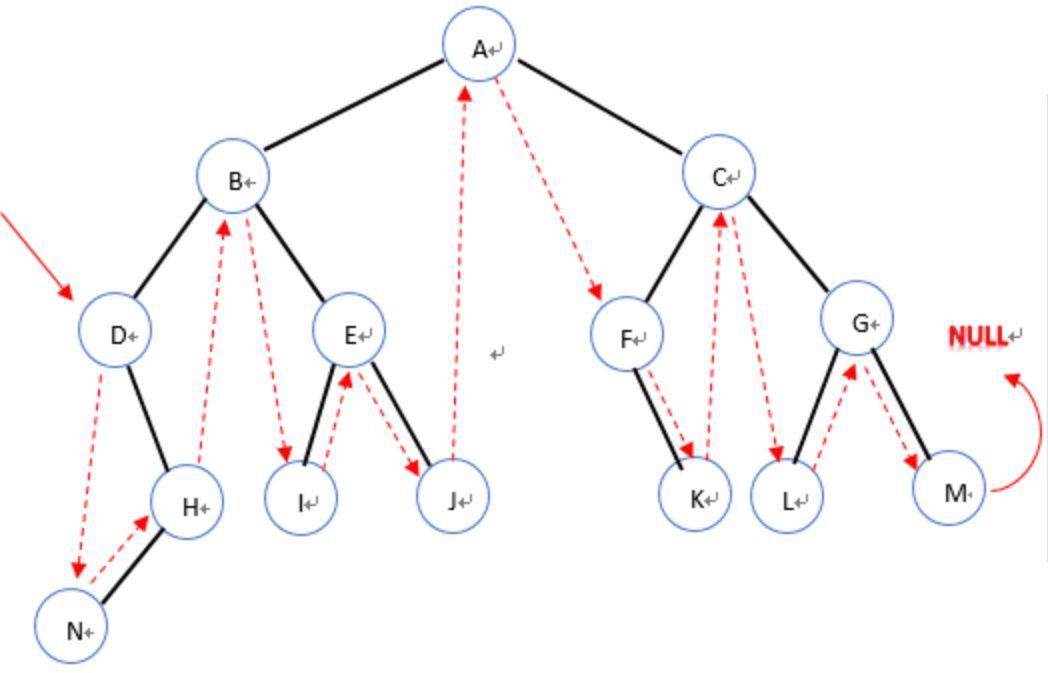
结合上图，我们可发现分成两大类：

1、有右子树的，那么下个结点就是右子树最左边的点；（eg：D，B，E，A，C，G）

2、没有右子树的，也可以分成两类：(a)是父节点左孩子（eg：N，I，L） ，那么父节点就是下一个节点 ；b)是父节点的右孩子（eg：H，J，K，M）找他的父节点的父节点的父节点…直到当前结点是其父节点的左孩子位置。如果没有eg：M，那么他就是尾节点。)。

代码实现(c++)

/*
struct TreeLinkNode {
    int val;
    struct TreeLinkNode *left;
    struct TreeLinkNode *right;
    struct TreeLinkNode *next;
    TreeLinkNode(int x) :val(x), left(NULL), right(NULL), next(NULL) {

    }
};
*/
class Solution {
public:
    TreeLinkNode* GetNext(TreeLinkNode* pNode)
    {
        if(pNode == NULL){
            return NULL;
        }
        TreeLinkNode* pNext = NULL;
        // 当前结点有右子树，那么它的下一个结点就是它的右子树中最左子结点
        if(pNode->right != NULL){
            TreeLinkNode* pRight = pNode->right;
            while(pRight->left != NULL){
                pRight = pRight-> left;
            }
            pNext = pRight;
        }
        // 当前结点无右子树，则需要找到一个是它父结点的左子树结点的结点
        else if(pNode->next != NULL){
            // 当前结点
            TreeLinkNode* pCur = pNode;
            // 父节点
            TreeLinkNode* pPar = pNode->next;
            while(pPar != NULL && pCur == pPar->right){
                pCur = pPar;
                pPar = pCur->next;
            }
            pNext = pPar;
        }
        return pNext;
    }
};