《剑指Offer》构建乘积数组

题目描述：

  给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0]A[1]...A[i-1]A[i+1]...A[n-1]。不能使用除法。

解题思路：

观察下公式，你会发现，B[i]公式中没有A[i]项，也就是说如果可以使用除法，就可以用公式B[i]=A[0]A[1].....*A[n-1]/A[i]来计算B[i]，但是题目要求不能使用，因此我们只能另想办法。

现在要求不能使用除法，只能用其他方法。一个直观的解法是用连乘n-1个数字得到B[i]。显然这个方法需要O(n*n)的时间复杂度。

好在还有更高效的算法。可以把B[i]=A[0]A[1].....A[i-1]A[i+1].....A[n-1]。看成A[0]A[1].....A[i-1]和A[i+1].....A[n-2]*A[n-1]两部分的乘积。

即通过A[i]项将B[i]分为两部分的乘积。效果如下图所示：

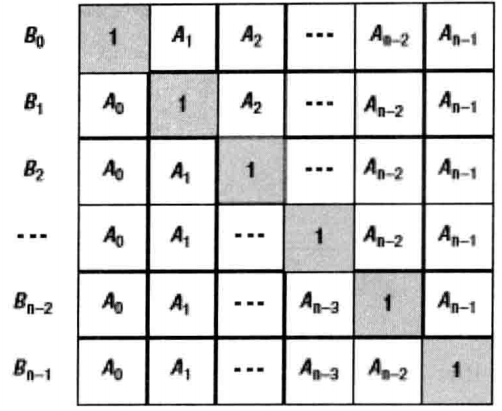
不妨设定C[i]=A[0]A[1]...A[i-1]，D[i]=A[i+1]...A[n-2]A[n-1]。C[i]可以用自上而下的顺序计算出来，即C[i]=C[i-1]A[i-1]。类似的，D[i]可以用自下而上的顺序计算出来，即D[i]=D[i+1]A[i+1]。

如果还是不明白，没有关系，直接看下代码，细细体会下就懂了。

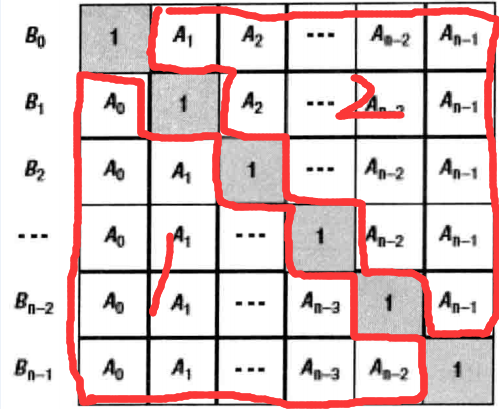
第一个for循环用来计算上图1范围的数，第二个for循环用来计算上图2范围的数。

代码实现(c++)

class Solution {
public:
    vector<int> multiply(const vector<int>& A) {
        int length = A.size();
        vector<int> B(length);
        if(length <= 0){
            return B;
        }
        B[0] = 1;
        for(int i = 1; i < length; i++){
            B[i] = B[i - 1] * A[i - 1];
        }
        int temp = 1;
        for(int i = length - 2; i >= 0; i--){
            temp *= A[i + 1];
            B[i] *= temp;
        }
        return B;
    }
};

代码实现(python)

python可以利用reduce方法快速求解。

# -*- coding:utf-8 -*-
class Solution:
    def multiply(self, A):
        # write code here
        B = []
        if len(A) == 0:
            return B
        else:
            for i in range(len(A)):
                tmp = A[i]
                A[i] = 1
                B.append(reduce(lambda x,y:x*y, A))
                A[i] = tmp
        return B