《剑指Offer》二叉树的深度

题目描述：

  输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。

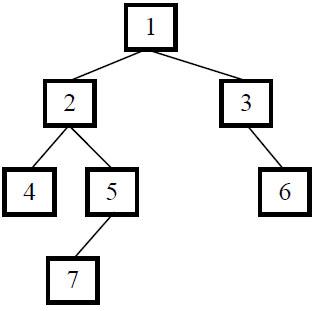
  例如下图中的二叉树的深度为4，因为它从根结点到叶结点最长的路径包含4个结点（从根结点1开始，经过结点2和结点5，最终到达叶结点7）。

解题思路：

  这道题蛮简单的，求二叉树的深度。可以是递归的方法，属于DFS（深度优先搜索）；另一种方法是按照层次遍历，属于BFS（广度优先搜索）。

　①如果一棵树只有一个结点，它的深度为1。

　 ②如果根结点只有左子树而没有右子树，那么树的深度应该是其左子树的深度加1；同样如果根结点只有右子树而没有左子树，那么树的深度应该是其右子树的深度加1。

　 ③如果既有右子树又有左子树，那该树的深度就是其左、右子树深度的较大值再加1。

　 比如在上图的二叉树中，根结点为1的树有左右两个子树，其左右子树的根结点分别为结点2和3。根结点为2的左子树的深度为3，而根结点为3的右子树的深度为2，因此根结点为1的树的深度就是4。

代码实现(c++)

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/
class Solution {
public:
    int TreeDepth(TreeNode* pRoot)
    {
        if(pRoot == NULL){
            return 0;
        }
        int left = TreeDepth(pRoot->left);
        int right = TreeDepth(pRoot->right);
        return (left > right) ? (left + 1) : (right + 1);
    }
};