题目:
数组中的数分为两组,给出一个算法,使得两个组的和的差的绝对值最小数组中的数的取值范围是0<x<100,元素个数也是大于0,小于100
比如a[]={2,4,5,6,7},得出的两组数{2,4,,6}和{5,7},abs(sum(a1)-sum(a2))=0;
比如{2,5,6,10},abs(sum(2,10)-sum(5,6))=1,所以得出的两组数分别为{2,10}和{5,,6}。
思路:
初看问题,感觉好像是个组合问题,通过暴力穷举解决问题。
但仔细想想,问题可以转换成,从数组中找出一组数据,使之尽可能等于数组和的一半。
这样一来是不是有点类似于0-1背包呢?是的,就是0-1背包问题。
条件:数组中的数就是背包问题的weight值,数组中的数也是背包问题的value值,即二者一样。
问题:背包里装哪些物品,使得其价值之和最接近总价值的一半。
于是通过背包问题来解决这道题就显得很简单了,下面简单陈述通过动态规划来求解0-1背包问题的思路。
假设V[i][j]表示从i件物品中选出重量为j的物品的最大价值,weight[i],value[i]分别代表第i件物品的重量和价值(在题目中,weight、value属于同一数组)。
动态转移方程为:
V[i][j]=V[i-1][j] if j<weight[i]
V[i][j]=max(V[i-1][j],V[i-1][j-weight[i]]+value[i]) if j>weight[i]
另外,如果想知道是由那几件物品组成的最大价值,可以从后往前回溯,当V[i][j]>V[i-1][j],说明第i件物品被加入(路径不唯一)。
代码:
#include <iostream>
#include <vector>
using namespace std;
int knapSack(int num,int C,const vector<int> weight,const vector<int> value,vector<int> &x);
int main()
{
int w[]={2,4,5,6,7};
int v[]={2,4,5,6,7};
int num=sizeof(w)/sizeof(w[0]);
vector<int> weight(w,w+num);
vector<int> value(v,v+num);
int C=12;
vector<int> x(num);
int total=knapSack(num,C,weight,value,x);
cout<<"Total weight is "<<total<<endl;
return 0;
}
int knapSack(int num,int C,const vector<int> weight,const vector<int> value,vector<int> &x){
vector<vector<int> > V(num+1,vector<int>(C+1));
for(int i=1;i<=num;i++){
for(int j=1;j<=C;j++){
if(j<weight[i-1])
V[i][j]=V[i-1][j];
else
V[i][j]=max(V[i-1][j],V[i-1][j-weight[i-1]]+value[i-1]);
}
}
cout<<"Dynamic Matrix: "<<endl;
for(int i=1;i<=num;i++){
for(int j=1;j<=C;j++){
cout<<V[i][j]<<" ";
}
cout<<endl;
}
int j=C;
for(int i=num;i>0;i--){
if(V[i][j]>V[i-1][j]){
x[i]=1;
j=j-weight[i-1];
}
else
x[i]=0;
}
cout<<"The articles chosen is: "<<endl;
for(int i=0;i<num;i++){
if(x[i])
cout<<i+1<<" ";
}
cout<<endl;
return V[num][C];
}
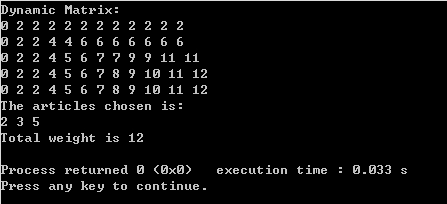
运行结果:

 菜鸟笔记
菜鸟笔记