一、二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

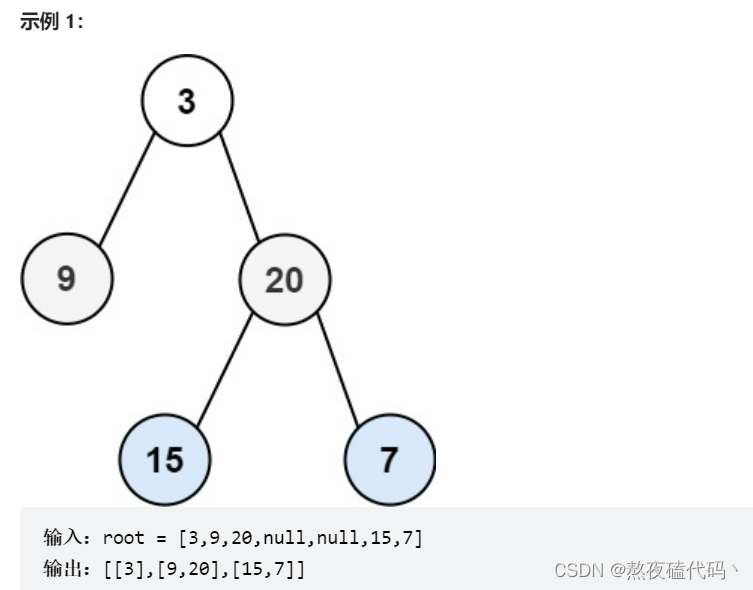
基本思路：
我们在二叉树的基本操作中已经实现了一次二叉树的层序遍历，但我们是直接进行打印，这里我们想把二叉树的每一层的结点放入List中，我们还是采用Queue来存储每一个结点，然后每次循环时，记录一下每层的元素个数，然后将每一层的结点放入list中，每次循环结束后将list放入List中。

public List<List<Integer>> levelOrder(TreeNode root) {
  
        //层序遍历
        List<List<Integer>> list = new ArrayList<>();
        if(root == null) {
  
            return list;
        }
        Queue<TreeNode> qu = new LinkedList<>();
        qu.offer(root);
        while(!qu.isEmpty()) {
  
            List<Integer> list1 = new ArrayList<>();
            int sz = qu.size();
            while(sz > 0) {
  
                TreeNode node = qu.poll();
                sz--;
                list1.add(node.val);
                if(node.left != null) {
  
                    qu.offer(node.left);
                }
                if(node.right != null) {
  
                    qu.offer(node.right);
                }
            }
            list.add(list1);
        } 
        return list;
    }

二、二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”


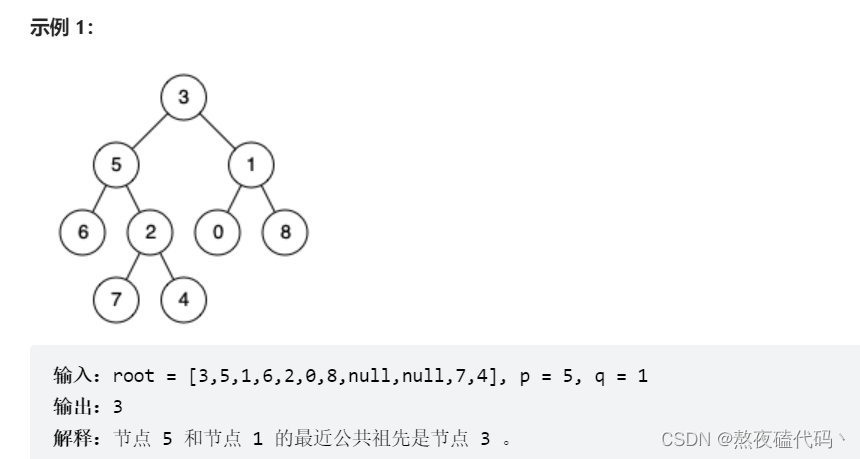
基本思路：
我们定义两个站，将根节点到p,q的路径全部放入两个栈中，就有点链表交点的感觉了，然后判断两个栈的大小，把多余元素先弹出，然后一起判断，直到相同结点为止。

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
  
        Stack<TreeNode> stack1 = new Stack<>();
        findPath(root,p,stack1);
        Stack<TreeNode> stack2 = new Stack<>();
        findPath(root,q,stack2);
        int sz1 = stack1.size();
        int sz2 = stack2.size();
        if(sz1 > sz2) {
  
            int sz = Math.abs(sz1 - sz2);
            while(sz > 0) {
  
                stack1.pop();
                sz--;
            }
        }else {
  
            int sz = Math.abs(sz1 - sz2);
            while(sz > 0) {
  
                stack2.pop();
                sz--;
            }
        }
        while (stack1.peek() != stack2.peek()) {
  
            stack1.pop();
            stack2.pop();
        }
        return stack1.peek();
    }
    public boolean findPath(TreeNode root, TreeNode node,Stack<TreeNode> stack) {
  
        if(root == null || node == null){
  
            return false;
        }
        stack.push(root);
        if(root == node) {
  
            return true;
        }
        boolean f1 = findPath(root.left,node,stack);
        if(f1 == true) {
  
            return true;
        }
        boolean f2 = findPath(root.right,node,stack);
        if(f2 == true) {
  
            return true;
        }
        stack.pop();
        return false;
    }

这样显然可以达到目的，但是时间复杂度有点高，我们能不能想一个时间复杂度比较低的解法。
我们先来认识一下：什么是二叉搜索树(二叉排序树）
二叉搜索树中，任何一结点的左节点总是小于该结点，右节点总是大于该节点。

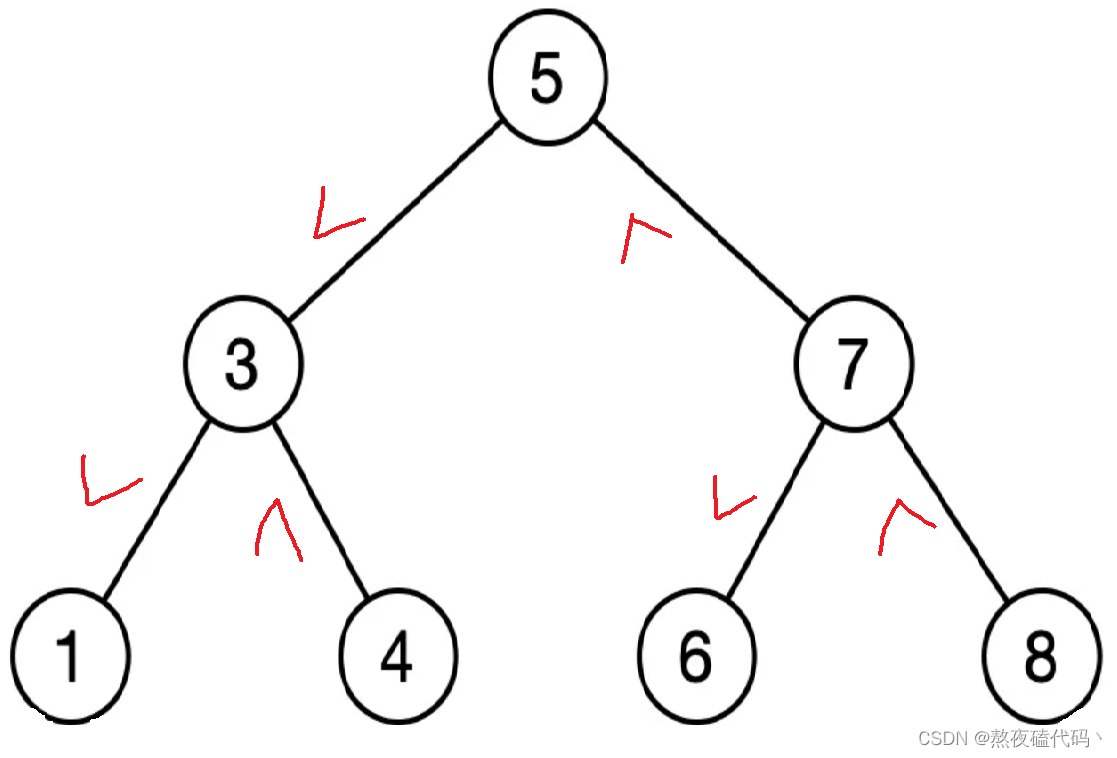
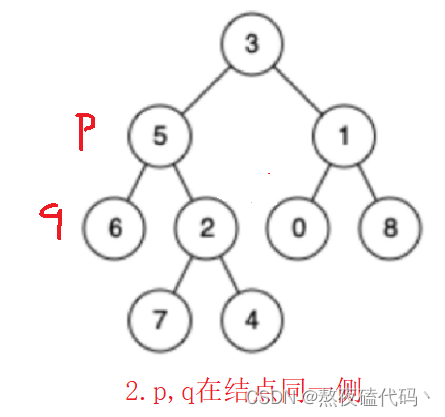
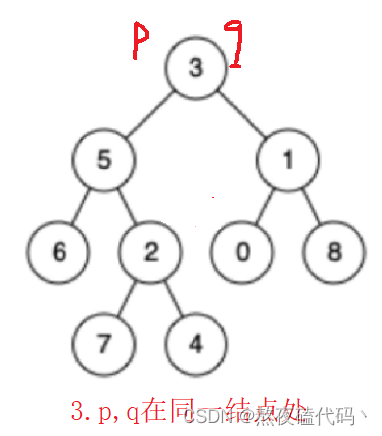
那我们最近公共祖先总共有几种情况呢？分为三种情况，1：p,q在同一位置 2：p,q在某一结点的两侧 3：p,q在某一结点的同一侧。

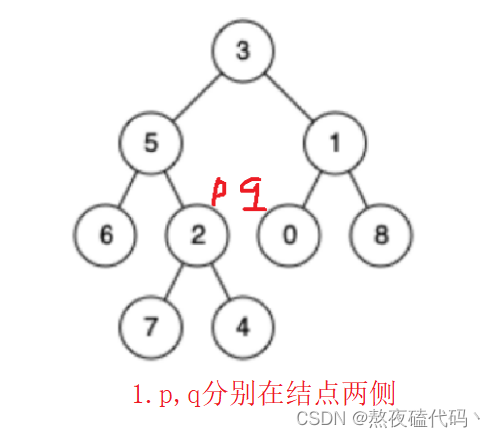
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
  
        if(root == null || p == null || q == null) {
  
            return null;
        }
        if(p == root || q == root) {
  
            return root;
        }
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        if(left != null && right != null) {
  
            return root;
        } else if(left == null) {
  
            return right;
        }else if(right == null) {
  
            return left;
        }else {
  
            return null;
        }
    }

三、二叉树遍历

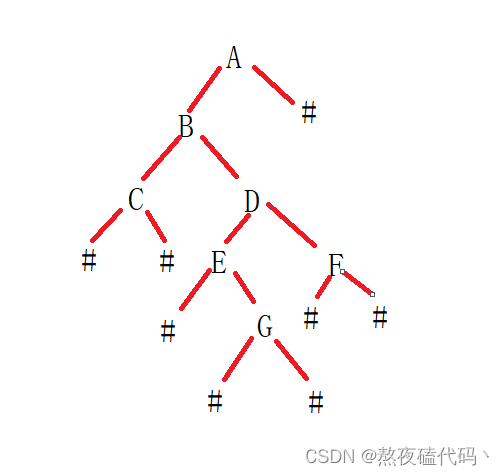
编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

我们可以看到这是一道较难题。
思路分析：
之前我们不是说过要想构建一个二叉树，必须直到中序遍历的结果，这道题只给了先序遍历的结果，能构建出来二叉树吗？我们可以发现题中给了空格的位置，那么我们就可以构建出来了，构建出来之后对二叉树进行中序遍历即可。因为先序遍历给我们的是字符串，我们要想取每一个结点，就得获取字符串的每一个字符，这里我们定义一个静态成员变量j记录先序遍历的每一个结点。

import java.util.Scanner;

class TreeNode {
  
    char val;
    TreeNode left;
    TreeNode right;

    public TreeNode(char val) {
  
        this.val = val;
    }
}
public class Main {
  
    public static void main(String[] args) {
  
        Scanner in = new Scanner(System.in);
        while (in.hasNextLine()) {
   
            String str = in.nextLine();
            TreeNode root = preSort(str);
            inOrder(root);
            System.out.println();
        }
    }
    public static void inOrder(TreeNode root) {
  
        if(root == null) {
  
            return;
        }
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }
    public static int j = 0;
    public static TreeNode preSort(String str) {
  
        TreeNode root = null;
        if(j < str.length()) {
  
            char c = str.charAt(j);
            if(c != '#') {
  
                root = new TreeNode(c);
                j++;
                root.left = preSort(str);
                root.right = preSort(str);
            }else {
  
                j++;
            }
        }
        return root;
    }
}

四、二叉搜索树与双向链表

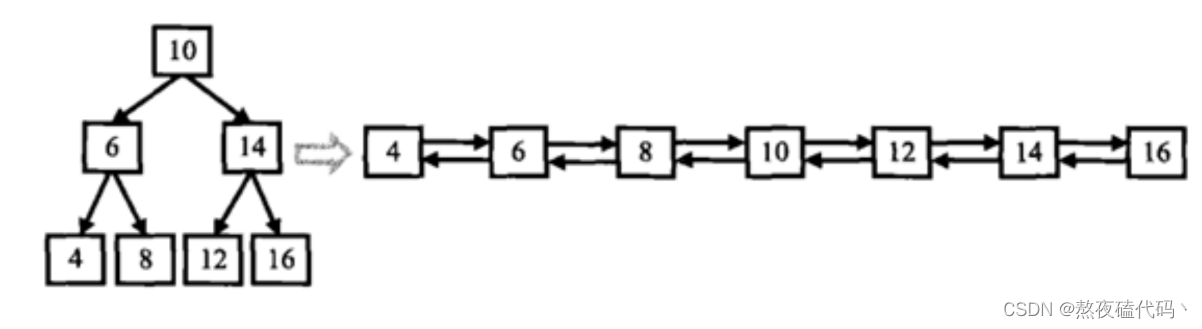
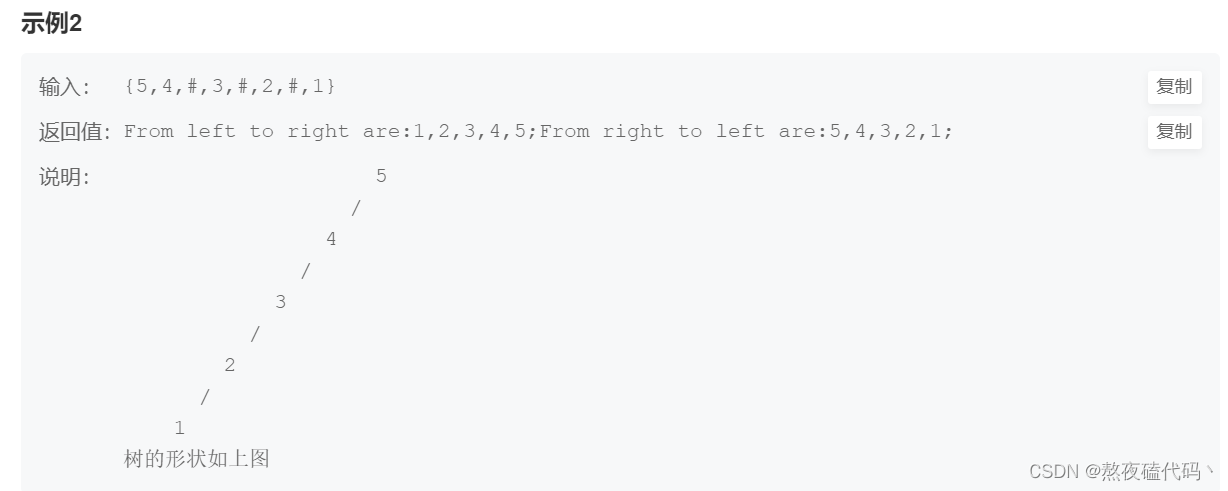
输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。如下图所示

注意:
1.要求不能创建任何新的结点，只能调整树中结点指针的指向。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode，有左右指针，其实可以看成一个双向链表的数据结构
4.你不用输出双向链表，程序会根据你的返回值自动打印输出


思路分析：
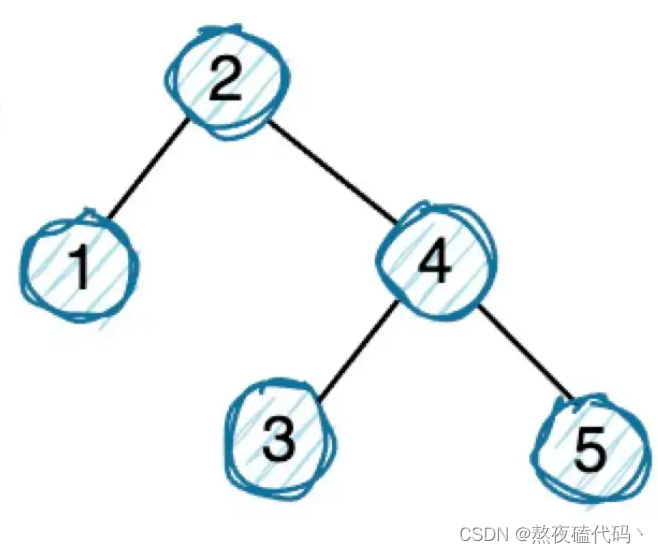
题目要求我们将一棵二叉搜索树转换为一个双链表，二叉树的left为链表的前驱，二叉树的right为链表的后驱。
这里我们采取前序遍历，在遍历到每一个结点的时候，改变结点的指向，将left指向前一结点,right指向后一结点。


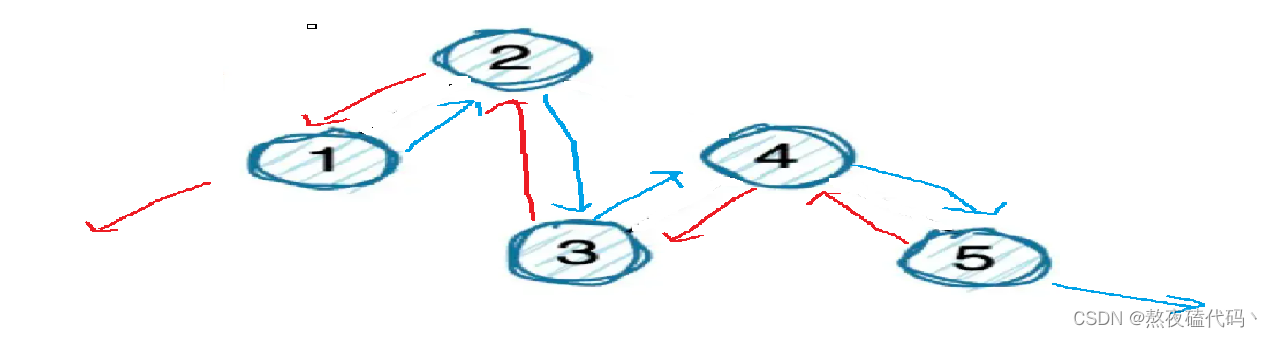
改变指向后那怎么找到头节点呢，因为我们的根节点已经成为链表中的某一结点，接下来我们将根节点往前遍历，直到.left为空为止，该节点就为头节点。

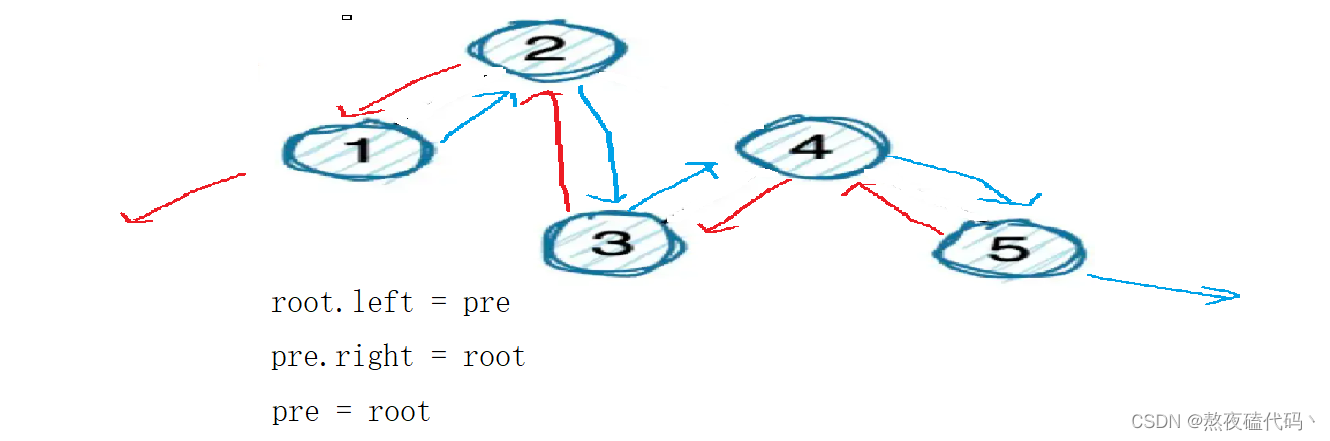
我们发现执行上面的代码就可以达到目的，但我们发现刚开始pre为空，没有right如果执行的话就会出现空指针异常，所以我们在执行时应该判断一下pre是否为空。

public TreeNode Convert(TreeNode pRootOfTree) {
  
        if(pRootOfTree == null) {
  
            return null;
        }
        createList(pRootOfTree);
        while(pRootOfTree.left != null) {
  
            pRootOfTree = pRootOfTree.left;
        }
        return pRootOfTree;
    }
    TreeNode pre = null;
    public void createList(TreeNode root) {
  
        if(root == null) {
  
            return;
        }
        createList(root.left);
        root.left = pre;
        if(pre != null) {
  
            pre.right = root;
        }
        pre = root;
        createList(root.right);
    }