递归算法时间复杂度分析-菜鸟笔记

时间复杂度：
一般情况下，算法中基本操作重复的次数就是问题规模n的某个函数f（n），进而分析f（n）随n的变化情况并确定T（n）的数量级。这里用‘o’来表示数量级，给出算法时间复杂度。
T（n）=o（f（n））；
它表示随问题规模n的增大，算法的执行时间增长率和f（n）增长率成正比，这称作算法的渐进时间复杂度。而我们一般情况下讨论的最坏的时间复杂度。
空间复杂度：
算法的空间复杂度并不是实际占用的空间，而是计算整个算法空间辅助空间单元的个数，与问题的规模没有关系。算法的空间复杂度S（n）定义为该算法所耗费空间的数量级。
S（n）=o（f（n））
若算法执行所需要的辅助空间相对于输入数据n而言是一个常数，则称这个算法空间复杂度辅助空间为o（1）；
递归算法空间复杂度：递归深度n*每次递归所要的辅助空间，如果每次递归所需要的辅助空间为常数，则递归空间复杂度o（n）。

递归算法分析

1利用数列知识

累加法：递推关系式为an+1−an=f(n)an+1−an=f(n)采用累加法。
累乘法：递推关系式为an+1an=f(n)an+1an=f(n)采用累乘法。
构造法：递推关系式为(1)aa+1=pan+qaa+1=pan+q，(2)aa+1=pan+qnaa+1=pan+qn，都可以通过恒等变形，构造出等差或等比数列，利用等差或等比数列的定义进行解题，其中的构造方法可通过待定系数法来进行。
和化项法：递推公式为Sn=f(n)Sn=f(n)或Sn=f(an)Sn=f(an)一般利用 an={S1，Sn−Sn−1，当n=1当n>=2an={S1，当n=1Sn−Sn−1，当n>=2
用特征方程求解递推方程（感觉比较生僻，不做解释）
迭代法： 从原始递推方程开始，反复将对于递推方程左边的函数用右边的等式代入，直到得到初值，然后将所得的结果进行化简。
例如在调用归并排序mergeSort(a,0,n-1)对数组a[0...n−1]a[0...n−1]排序时，执行时间T(n)T(n)的递推关系式为：
T(n)={O(1)，2T(n2)+O(n)，当n=1当n>=2T(n)={O(1)，当n=12T(n2)+O(n)，当n>=2

其中，O(n)O(n)为merge()所需要的时间，设为cncn（c为正常量）。因此：

T(n)=2T(n2)+cn=2(2T(n4)+cn2)+cn=22T(n4)+2cn=23T(n8)+3cn=...=2kT(n2k)+kcn=nO(1)+cnlog2n=O(nlog2n),(假设n=2k,则k=log2n)T(n)=2T(n2)+cn=2(2T(n4)+cn2)+cn=22T(n4)+2cn=23T(n8)+3cn=...=2kT(n2k)+kcn=nO(1)+cnlog2⁡n=O(nlog2⁡n),(假设n=2k,则k=log2⁡n)

忽略求解细节。在我们求解递归式时，因为最终是要求得一个时间上限，所以在求解时常常省略一些细节。比如mergeSort(a,0,n-1)运行时间的实际递归式应该是：

T(n)={O(1)，T(⌈n2⌉)+T(⌊n2⌋)+O(n)，当n=1当n>=2T(n)={O(1)，当n=1T(⌈n2⌉)+T(⌊n2⌋)+O(n)，当n>=2

但我们忽略这些上取整、下取整以及边界条件，甚至假设问题规模n=2kn=2k，这都是为方便求解而忽略的细节。经验和一些定理告诉我们，这些细节不会影响算法时间复杂度的渐近界。

类似的，我们也可以用迭代法求解汉诺塔递归求解时的时间复杂度。但遗憾的是，迭代法一般适用于一阶的递推方程。对于二阶及以上（即T(n)依赖它前面更多个递归项T(n)依赖它前面更多个递归项）的递推方程，迭代法将导致迭代后的项太多，从而使得求和公式过于复杂，因此需要将递推方程化简，利用差消法等技巧将高阶递推方程化为一阶递推方程。如在求快速排序算法平均时间复杂度T(n)T(n)的递推方程，T(n)T(n)依赖T(n−1)、T(n−2)、...、T(1)T(n−1)、T(n−2)、...、T(1)等所有的项，这样的递推方程也称为全部历史递推方程。（这里省略快速排序算法平均复杂度T(n)的求解过程）

小结：上面6种递推关系是高中、本科知识，在此重点介绍了迭代法，其它几种方法虽未在本篇中使用，但可以加深对递推式求解的认识。

2代入法

代入法实质上就是数学归纳法，因此求递推式分为两步：

猜测解的形式；
用数学归纳法求出解中的常数，并证明解是正确的。

遗憾的是并不存在通用的方法来猜测递归式的正确解，需要凭借经验，偶尔还需要创造力。即使猜出了递归式解的渐近界，也有可能在数学归纳证明时莫名其妙的失败。正是由于该方法技术细节较为难掌握，因此这个方法不适合用来求解递归方程，反而比较适合作为其他方法检验手段。在此不做总结。可以翻阅《算法导论》进行学习。

3递归树

递归树是一棵结点带权值的树。初始的递归树只有一个结点，它的权标记为T(n)T(n)；然后按照递归树的迭代规则不断进行迭代，每迭代一次递归树就增加一层，直到树中不再含有权值为函数的结点（即叶结点都为T(1)T(1)）。下面以递归方程

T(n)={O(1)，2T(n2)+O(n)，当n=1当n>=2;(假设n=2k,则k=log2n)T(n)={O(1)，当n=12T(n2)+O(n)，当n>=2;(假设n=2k,则k=log2⁡n)

来讲述递归树的迭代规则。

第一步： 把根结点T(n)T(n)用根是cncn、左结点为T(n2)T(n2)、右结点为T(n2)T(n2)的子树代替（即：以分解、合并子问题需要的代价为根，分解得到的子问题为叶的子树。其中常量c代表求解规模为1的问题所需的时间）；（如下如(a)→(b)(a)→(b)）

第二步：把叶结点按照“第一步”的方式展开；T(n2)T(n2)用根是cn/2cn/2、左节点为T(n4)T(n4)、右结点为T(n4)T(n4)的子树代替。（如下如(b)→(c)(b)→(c)）

第三步：反复按照“第一步”的方式迭代，每迭代一次递归树就增加一层，直到树中不再含有权值为函数的结点（即叶结点都为T(1)T(1)）。（如下如(c)→(d)(c)→(d)）

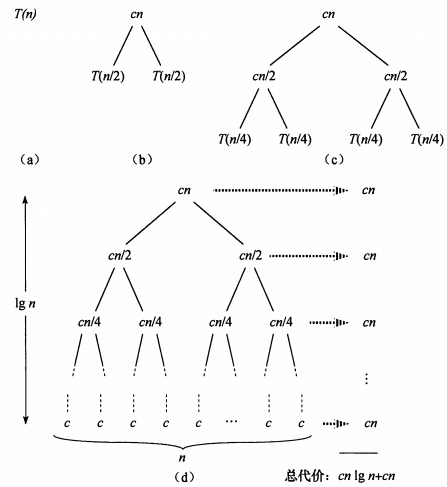
在得到递归树后，将树中每层中的代价求和，得到每层代价，然后将所有层的代价求和，得到所有层次的递归调用的总代价。在上图(d)部分中，完全展开的递归树高度为lgnlg⁡n(树高为根结点到叶结点最长简单路径上边的数目)，所有递归树具有lgn+1lg⁡n+1层，所以总代价为cn∗(lgn+1)cn∗(lg⁡n+1)，所有时间复杂度为Θ(nlgn)Θ(nlg⁡n)。

总结：递归树模型求解递归方程，本质上就是迭代思想的应用，利用递归方程迭代展开过程构造对应的递归树，然后把每层的时间代价进行求和。不过递归树模型更直观，同时递归树也克服了二阶及更高阶递推方程不方便迭代展开的痛点。

4主方法求解递推式

主方法为如下形式的递归式提供了一种“菜谱”式的求解方法，如下所示

T(n)=aT(n/b)+f(n)T(n)=aT(n/b)+f(n)

其中a≥1a≥1和b>1b>1是常数，f(n)f(n)是渐近正函数。这个递推式将规模为n的问题分解为a个子问题，每个子问题的规模为n/bn/b，a个子问题递归地求解，每个花费时间T(n/b)T(n/b)。函数f(n)f(n)包含了问题分解和子问题解合并的代价。同样，这个递归式也没有考虑上取整、下取整、边界条件等，结果不会影响递归式的渐近性质。

定理4.1(主定理) 令a≥1和b>1是常数，f(n)f(n)是一个函数，T(n)T(n)是定义在非负整数上的递归式：

T(n)=aT(n/b)+f(n)T(n)=aT(n/b)+f(n)

其中我们将n/bn/b解释为⌊n/b⌋⌊n/b⌋或⌈n/b⌉⌈n/b⌉。那么T(n)T(n)有如下渐近界：

1. 若对某个常数ε>0ε>0有f(n)=O(n(logba)−ε)f(n)=O(n(logb⁡a)−ε)，则T(n)=Θ(nlogba)T(n)=Θ(nlogb⁡a)

2. 若f(n)=Θ(nlogba)f(n)=Θ(nlogb⁡a)，则T(n)=Θ(nlogbalgn)T(n)=Θ(nlogb⁡alg⁡n)。

3. 若对某个常数ε>0ε>0有f(n)=Ω(n(logba)+ε)f(n)=Ω(n(logb⁡a)+ε)，且对某个常数c<1c<1和所有足够大的n有af(n/b)≤cf(n)af(n/b)≤cf(n)，则T(n)=Θ(f(n))T(n)=Θ(f(n))

在使用主定理之前，要比较f(n)和(nlogba)f(n)和(nlogb⁡a)的大小，这个大小不是算术意义上的大小比较，而是要在多项式意义上比较。以上三种情况在多项式意义上并未覆盖f(n)f(n)的所有可能性。情况1和情况2之间有一定间隙；情况2和情况3之间也有一定间隙。如果f(n)落在这两个间隙中，或者情况3中正则条件不成立，就不能使用主方法来求递归式。
如在递归式：T(n)=2T(n/2)+nlgnT(n)=2T(n/2)+nlg⁡n中，因为 nlogba=n0ε>0当n足够大时，均有nε>lgnnε>lg⁡n。所以找不到这样 ε>0ε>0，该递归式落入了情况2和情况3之间的间隙，不能使用主定理。
最后给出主定理应用的几个练习题：

具体举例分析：

【代入法】代入法首先要对这个问题的时间复杂度做出预测，然后将预测带入原来的递归方程，如果没有出现矛盾，则是可能的解，最后用数学归纳法证明。

　　【举例】我们有如下的递归问题：T(n)=4T(n/2)+O(n)，我们首先预测时间复杂度为O(n2),不妨设T(n)=kn2（其中k为常数），将该结果带入方程中可得：左=kn2，右=4k(n/2)2+O(n)=kn2+O(n),由于n2的阶高于n的阶，因而左右两边是相等的，接下来用数学归纳法进行验证即可。

　　【迭代法】迭代法就是迭代的展开方程的右边，直到没有可以迭代的项为止，这时通过对右边的和进行估算来估计方程的解。比较适用于分治问题的求解，为方便讨论起见，给出其递归方程的一般形式：

　　【举例】下面我们以一个简单的例子来说明：T(n)=2T(n/2)+n2,迭代过程如下：

　　容易知道，直到n/2^(i+1)=1时，递归过程结束，这时我们计算如下：

　　到这里我们知道该算法的时间复杂度为O(n2)，上面的计算中，我们可以直接使用无穷等比数列的公式，不用考虑项数i的约束，实际上这两种方法计算的结果是完全等价的，有兴趣的同学可以自行验证。

　　【公式法】这个方法针对形如：T(n) = aT(n/b) + f(n)的递归方程。这种递归方程是分治法的时间复杂性所满足的递归关系，即一个规模为n的问题被分成规模均为n/b的a个子问题，递归地求解这a个子问题，然后通过对这a个子问题的解的综合，得到原问题的解。这种方法是对于分治问题最好的解法，我们先给出如下的公式：

　　公式记忆：我们实际上是比较n^logba和f(n)的阶，如果他们不等，那么T(n)取他们中的较大者，如果他们的阶相等，那么我们就将他们的任意一个乘以logn就可以了。按照这个公式，我们可以计算【迭代法】中提到的例子：O(f(n))=O(n2),容易计算另外一个的阶是O(n),他们不等，所以取较大的阶O(n2)。太简单了，不是吗？

　　需要注意：上面的公式并不包含所有的情况，比如第一种和第二种情况之间并不包含下面这种情况：f(n)是小于前者，但是并不是多项式的小于前者。同样后两种的情况也并不包含所有的情况。为了好理解与运用的情况下，笔者将公式表述成如上的情况，但是并不是很严谨，关于该公式的严密讨论，请看这里。但是公式的不包含的情况，我们很少很少碰到，上面的公式适用范围很广泛的。

　　特别地，对于我们经常碰到的，当f(n)=0时，我们有：