红黑树
注:在学习红黑树之前,建议先对AVL树具备一定的了解
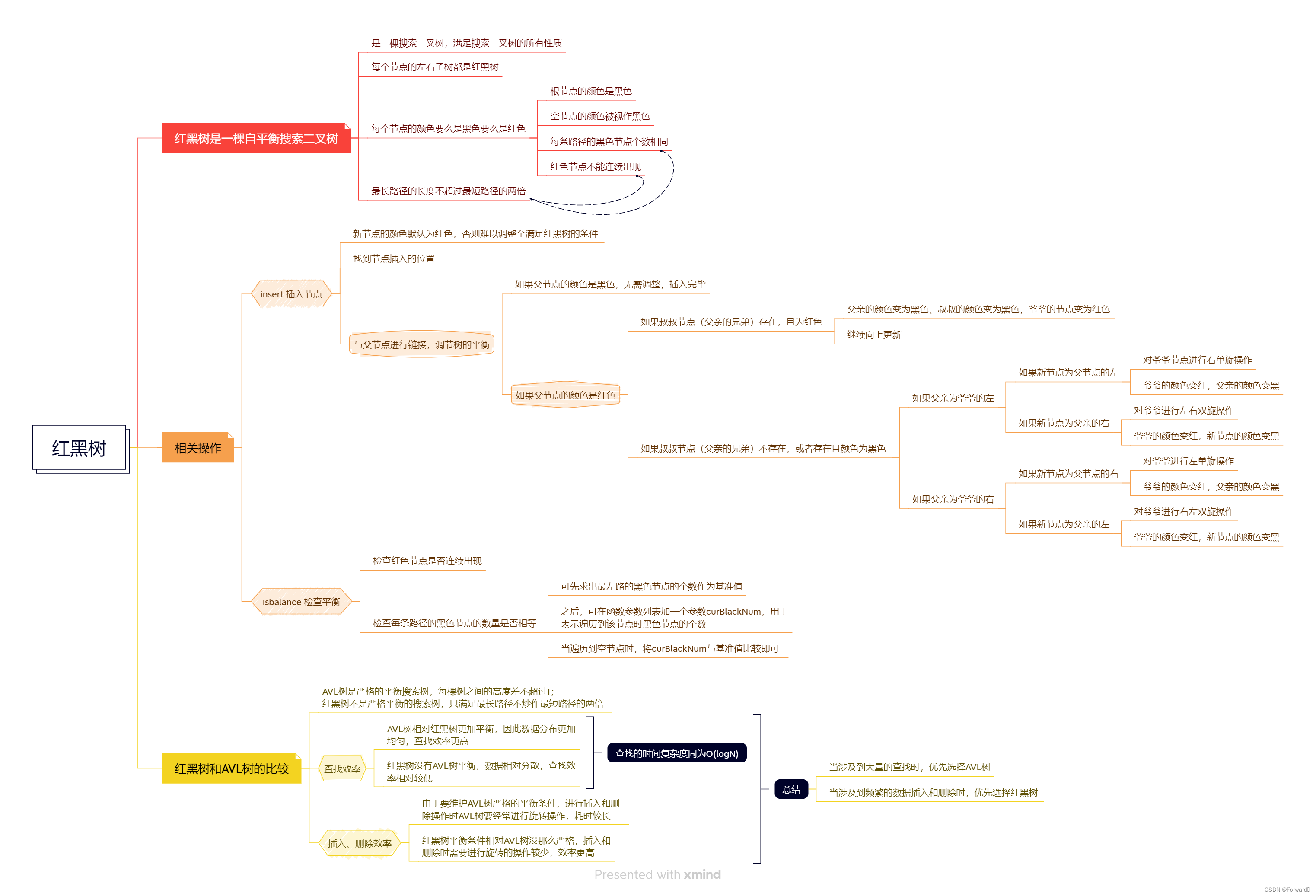
1. 红黑树的性质

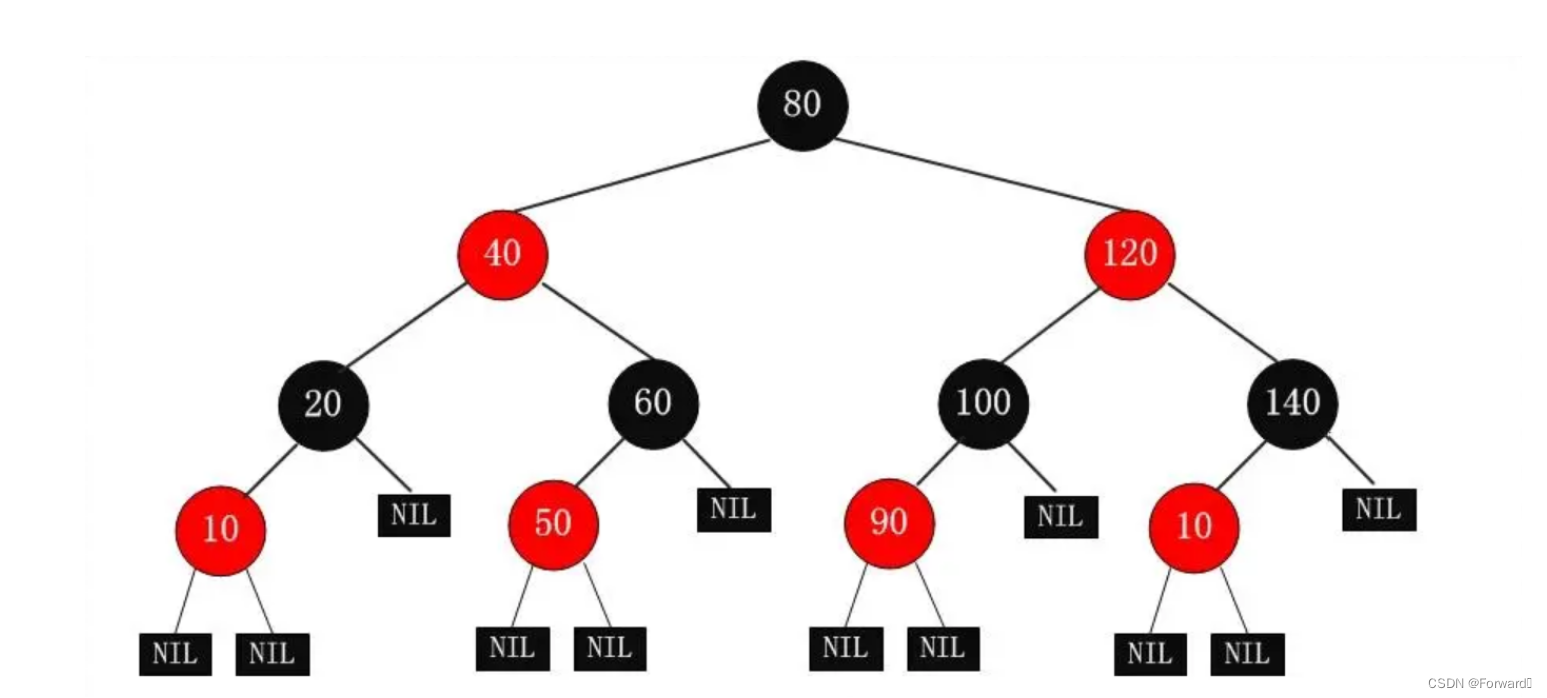
和AVL树一样,红黑树也是一棵自平衡的搜索二叉树
如上图,就是一棵经典的红黑树,以下是他的性质:
- 红黑树同样是一棵搜索二叉树,其满足搜索二叉树的所有性质:
每个节点的左右子树都是一棵搜索二叉树
左孩子的键值比父亲的小;右孩子的键值比父亲的大
红黑树的每个节点的左右子树也都是红黑树
红黑树的每个节点都有一个颜色,且要么是红色要么是黑色;空节点被视作黑色节点
红黑树的根节点的颜色必须是黑色
红黑树每条路径的黑色节点个数必须相等
红黑树的红色节点不能连续出现
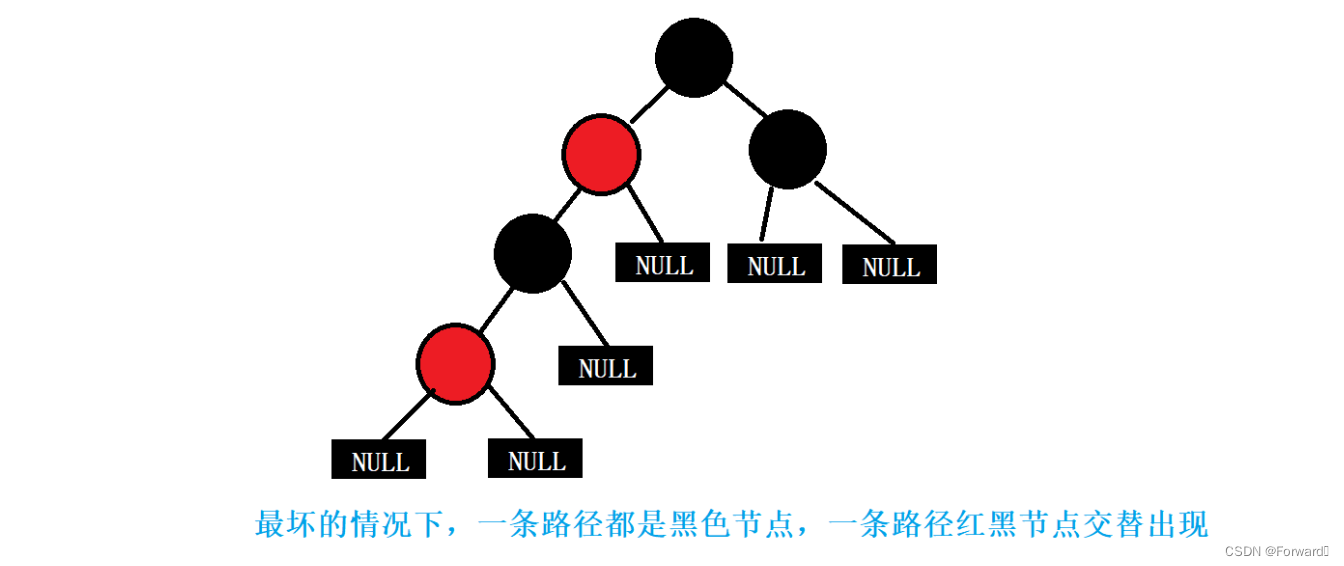
由性质5和性质6,我么可以推导出红黑树的平衡特性:
红黑树的最长路径的长度不会超过最短路径的两倍
2. 了解操作
2.1 红黑树节点类的定义:
//定义一个枚举类,用于表示颜色
enum Color
{
RED,
BLACK
};
//默认该红黑树的存储模型为key_value型
template<class K, class V>
struct RBTreeNode
{
typedef RBTreeNode<K, V> Node;
Node* _parent = nullptr;
Node* _left = nullptr;
Node* _right = nullptr;
pair<K, V> _kv;
Color _color = RED; //节点默默的颜色为红色
RBTreeNode(const pair<K, V> kv)
: _kv(kv)
{
}
};
2.2 插入节点
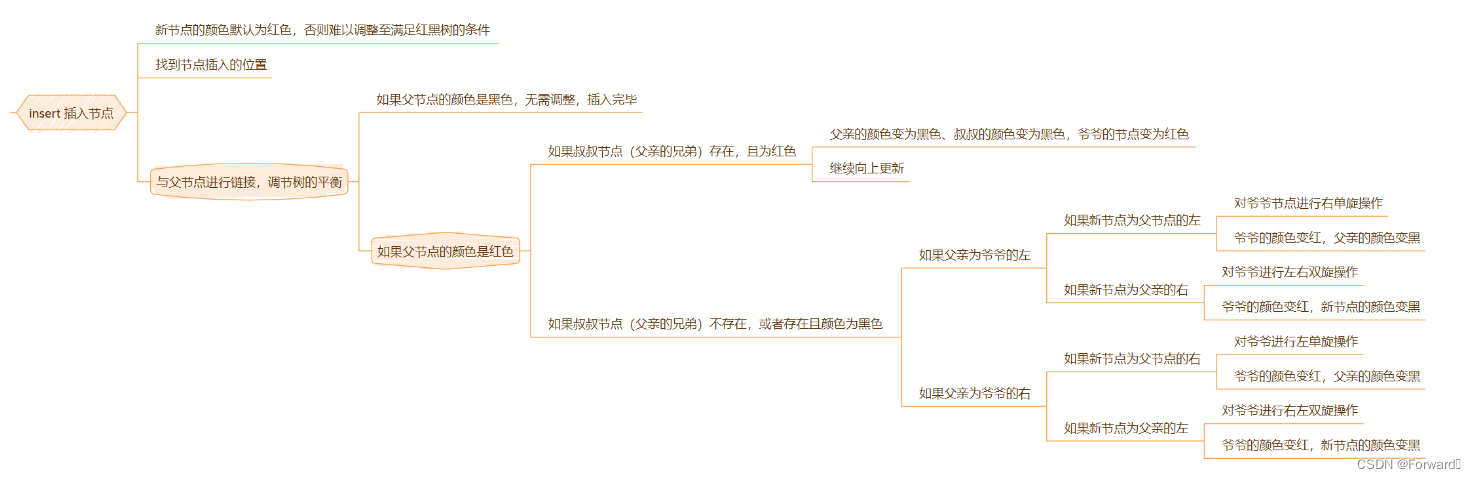
2.1.1 找到插入位置
既然红黑树也是一棵搜索二叉树,那么在插入新节点之前,首先肯定也要找到插入位置:
bool insert(const pair<K, V> kv)
{
//如果原来是一棵空树
if (_root == nullptr)
{
_root = new Node(kv);
_root->_color = BLACK;
return true;
}
//找到插入位置
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
parent = cur;
if (cur->_kv.first > kv.first)
cur = cur->_left;
else if (cur->_kv.first < kv.first)
cur = cur->_right;
else
return false;
}
cur = new Node(kv);
cur->_parent = parent;
if (cur->_kv.first > parent->_kv.first)
parent->_right = cur;
else
parent->_left = cur;
//……………………
}
2.1.2 新节点颜色
红黑树的每个节点的颜色要么是红色,要么是黑色,那么我们新插入的节点应该是什么颜色?红色,还是黑色,还是红色黑色都可能呢?
我么可以进行假设:
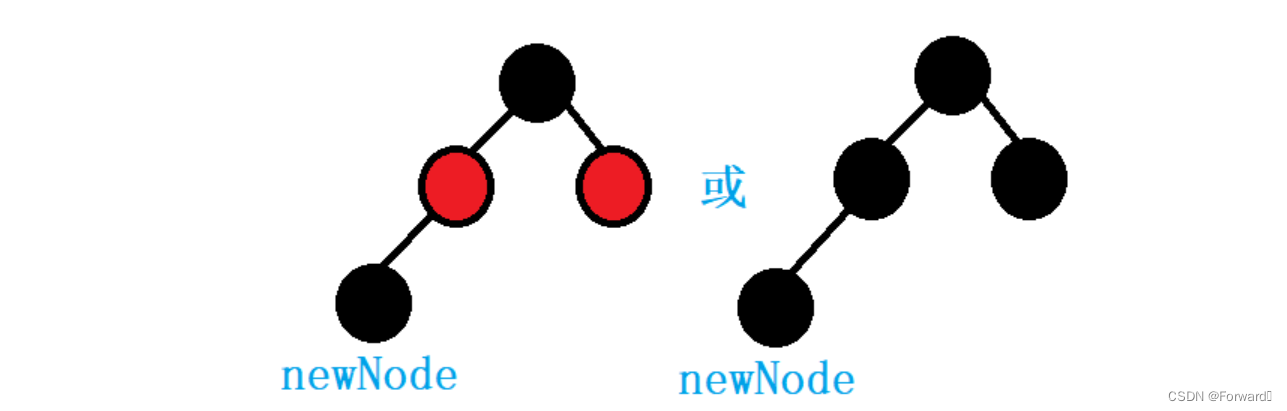
假设新节点的颜色是黑色,如下图:
可以看到,如论黑色节点插入到哪个位置,红黑树的条件都会被打破
- 这是因为:插入之前就是一棵红黑树,那么每条路径的黑色节点个数就一定相同
- 此时在任意位置插入一个黑色节点,就肯定会使一条路径的黑色节点个数多余其他路径,从而破坏红黑树的条件
可见,如果新节点的颜色是黑色,我们是很难在插入后将其还原到满足红黑树的条件的
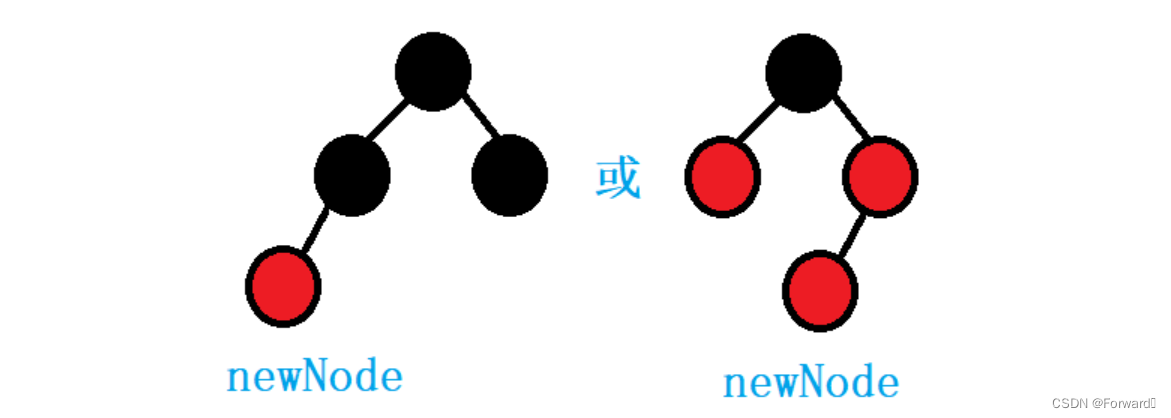
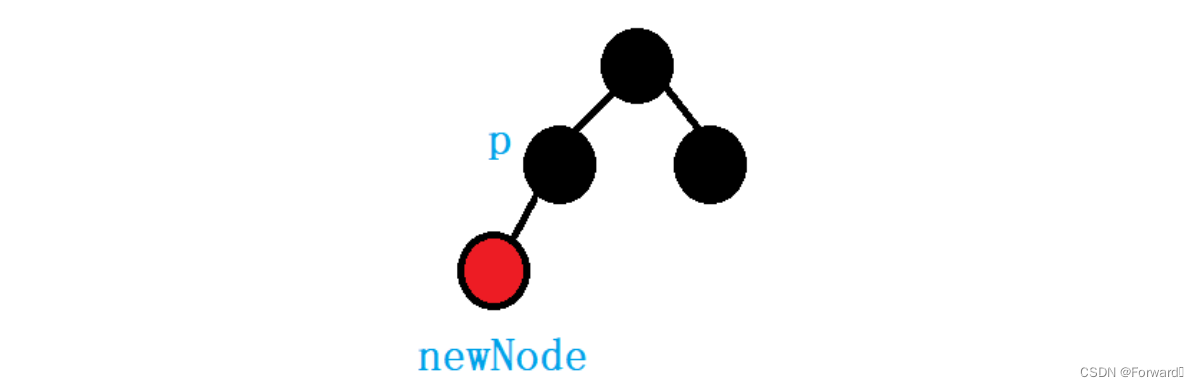
假设新节点的颜色是红色,如下图:
从图中可以看到:
- 如果父节点的颜色是黑色,那么插入一个红色节点并不会破坏红黑树的条件
- 如果父节点的颜色是红色,那么就会出现“出现连续红色节点”的情况,需要做出调整
总结:
- 虽然插入黑色节点和红色节点都可能会导致红黑树的条件被破坏,但是相较于插入黑色节点必定会破坏红黑树的条件,插入红色节点只会在其父节点也是红色时才会破坏红黑树的条件
- 因此,插入红色节点代价更小,即新节点的颜色默认为红色
接下来,我们就来分析父节点为红色或黑色时的不同插入情况
注意:
红黑树的形态无穷无尽,博主不可能将每种红黑树的插入情况都列举出来
但是,这些所有的情况都可以被分为父节点为黑色和父节点为红色这两类
博主在后面的分析会以一棵具体的红黑树来做示例,讲述节点的插入和后续颜色的调整。至于其他形态的红黑树,只要插入时的情况被归类为某一特定的情况,都可以用相同的方法处理,大家学会处理方法即可
2.1.3 父节点为黑色
插入新节点之前该树就是一棵红黑树,如果新节点的父节点的颜色是黑色,那么插入一个红色节点并不会影响到红黑树的条件
- 红色节点没有连续出现
- 每条路径的黑色节点个数仍然相等
因此,如果新节点的父节点为黑色,插入流程结束
2.1.4 父节点为红色
如果父节点的颜色为红色,那么就要分叔叔节点为红色以及叔叔节点不存在/叔叔节点为黑色这两种情况来讨论
注意:
以下涉及关于旋转的操作均已在AVL树中提及,下面只会讲述大概的步骤,并提供代码,不会做详细讲解
2.1.4.1 叔叔节点为红色

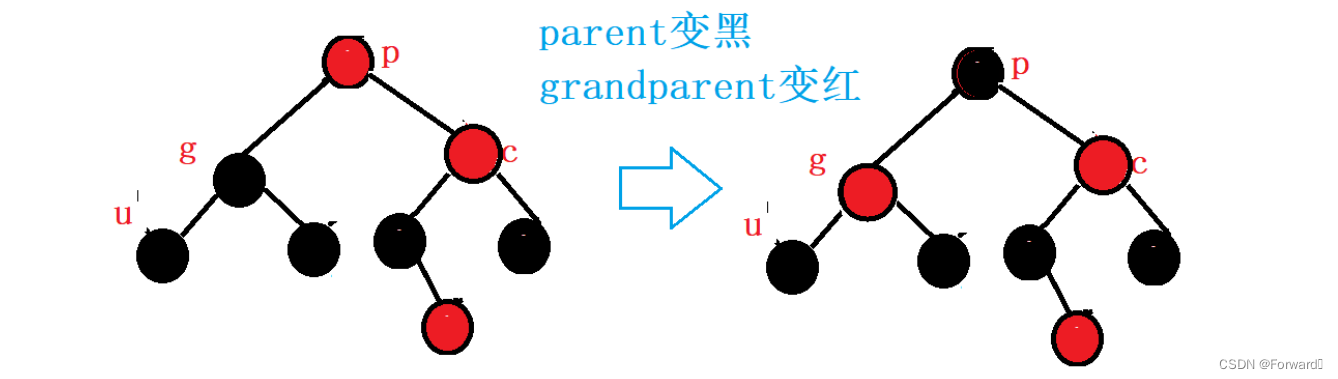
此时,为了使红色节点不连续出现,并且保持每条路径的黑色节点个数相等,我们需要对部分节点的颜色进行调整:
爷爷节点的颜色改为红色
叔叔节点和父节点的颜色改为黑色
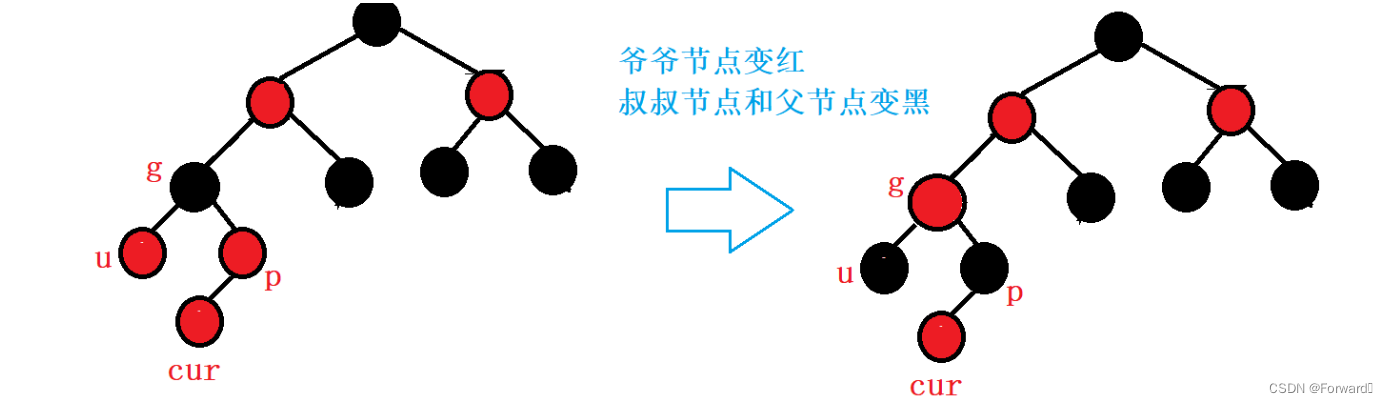
调节过后,如果爷爷节点的父亲仍为红色,则要继续向上调节

需要注意,上图中的爷爷节点就是整棵树的根节点,而规定红黑树的根节点是黑色的,因此调整完过后需要注意将根节点改为黑色
2.1.4.2 叔叔节点不存在/叔叔节点为黑色
在向上调整的过程中,我们可能会遇到叔叔节点不存在或者叔叔节点为黑色的情况:

此时,我们不能像叔叔节点为红色的情况一样,简单的将父节点变黑,爷爷节点变红来解决问题:
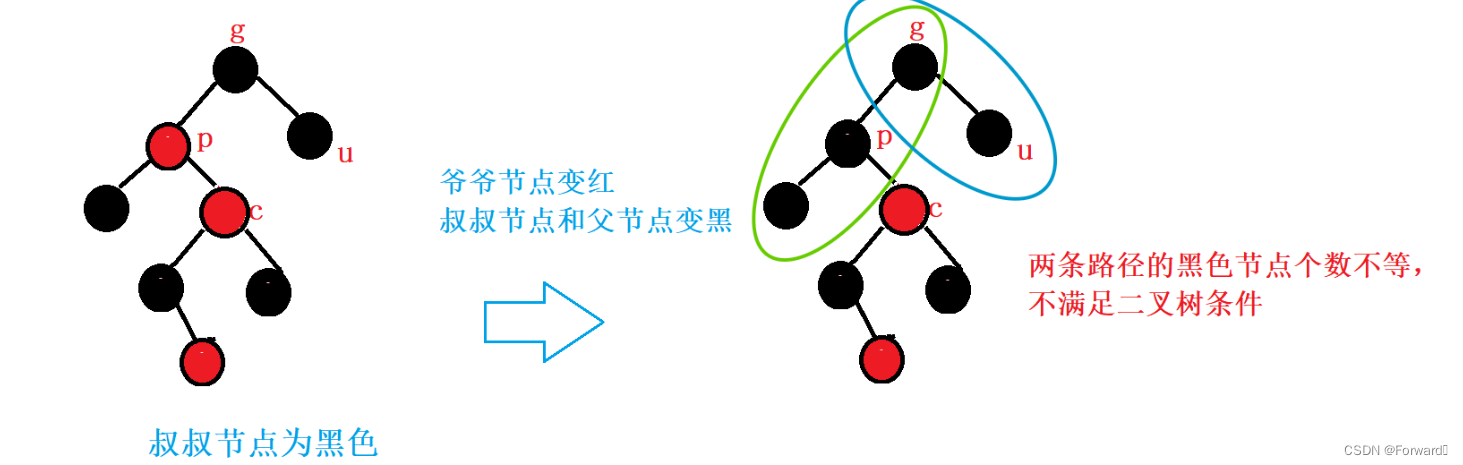
针对这种情况,我们需要根据parent节点相对grandparent的位置以及cur节点相对parent节点的位置,通过旋转来解决问题:
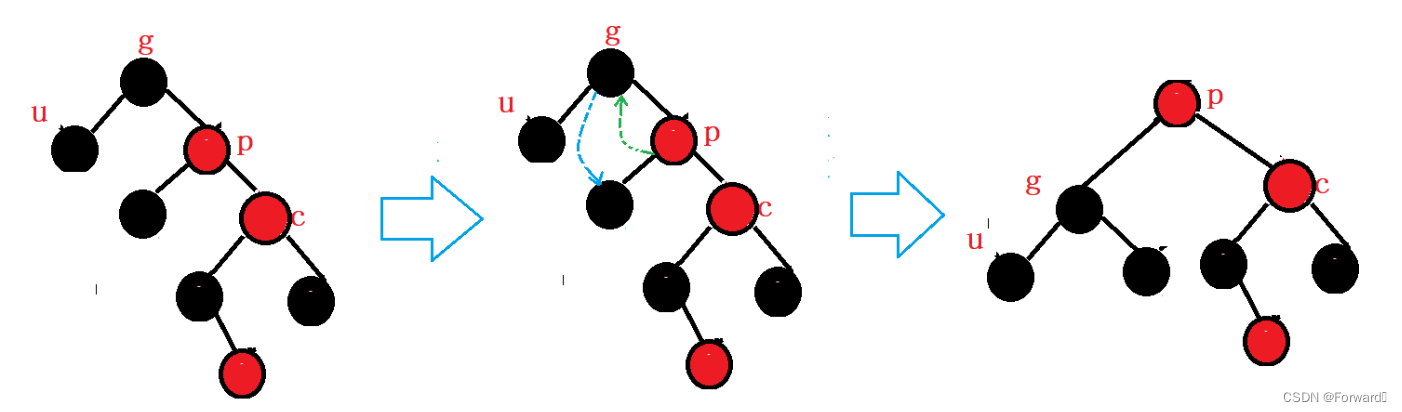
2.1.4.2.1 父节点parent为爷爷节点grandparent的左
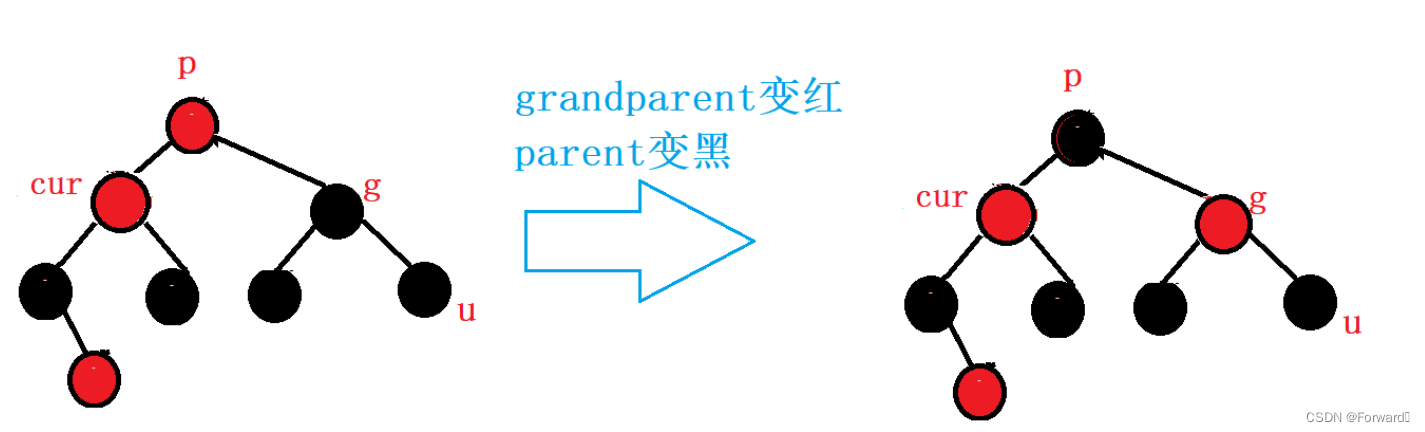
情况一:cur为parent的左
如图:
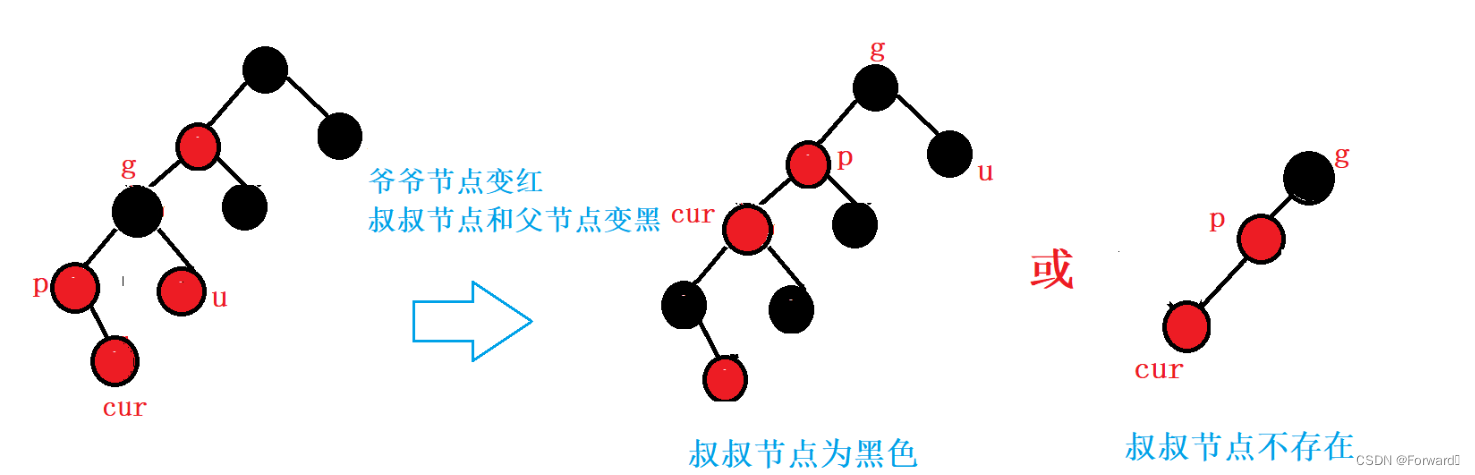
此时,我们需要对
grandparnet节点进行右单旋操作:
将
parent的右孩子链接给grandparent的左孩子将
grandparent链接给parent的右孩子
最后,调节节点的颜色,使其满足红黑树的条件:
grandparent的颜色红parnet的颜色变黑
对于叔叔节点不存在的情况,也执行相同的操作:
调整完毕
需要清楚的是
调整后和插入节点前相比,该树每条路径的黑色节点的总个数并没有被改变,并且新的根为黑色
如果该树是其他树的子树,尽管插入了一个节点,但是经过旋转调整过后并不会影响到其他节点,因此可以直接结束插入过程
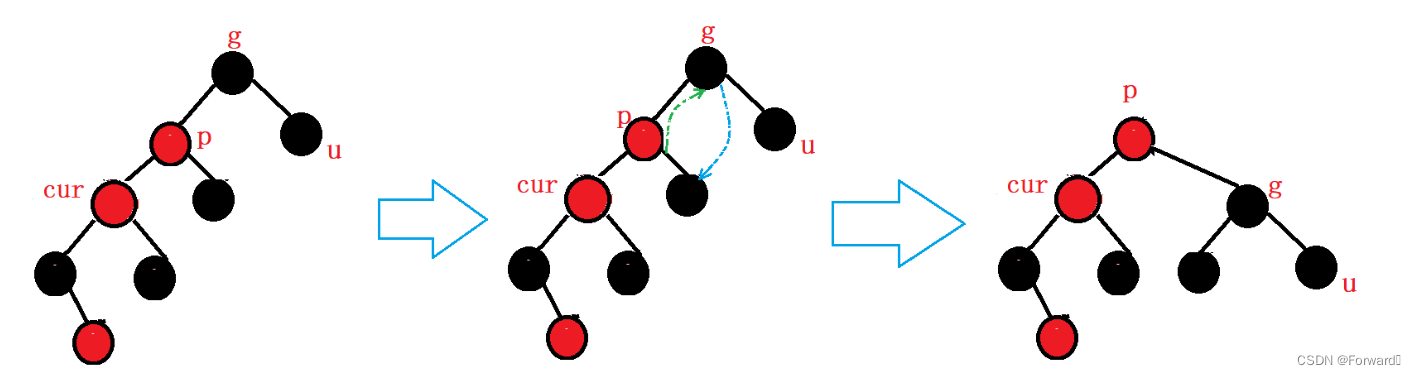
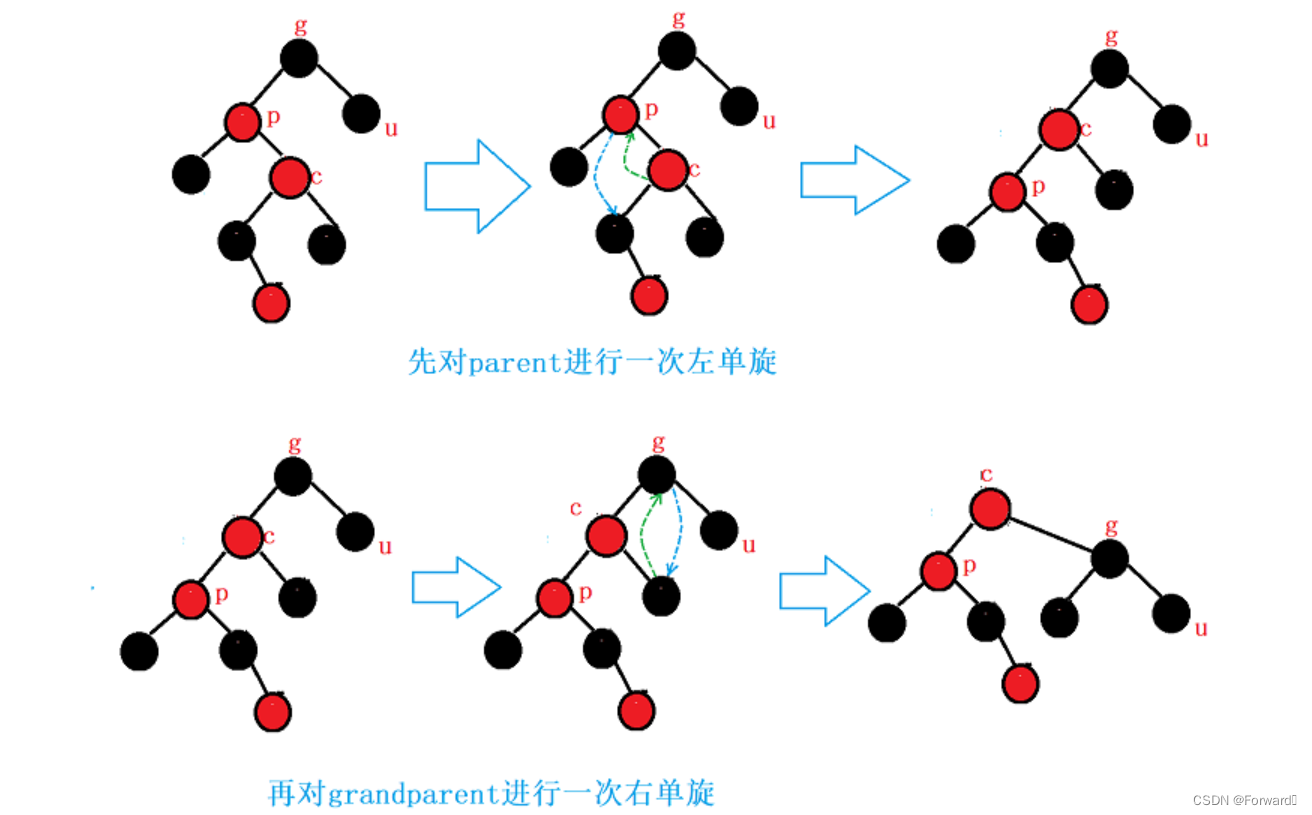
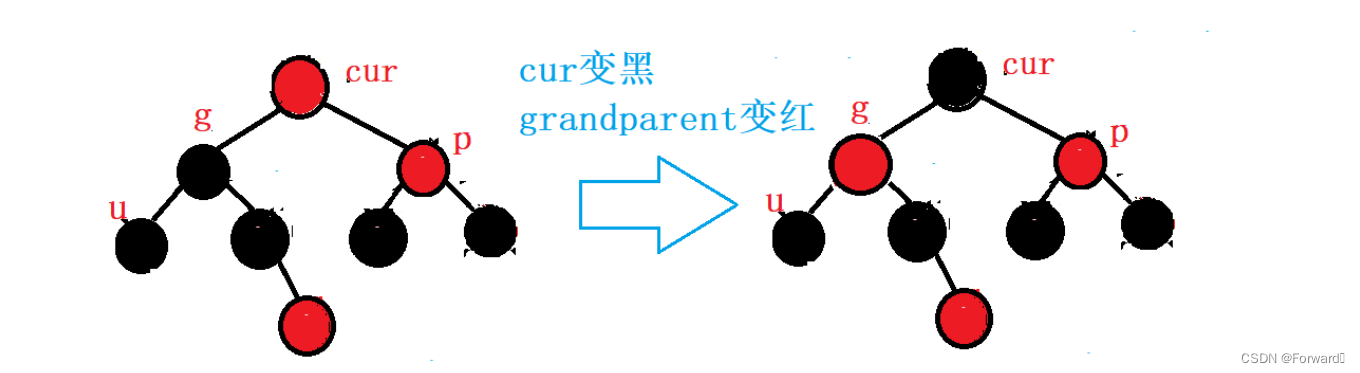
情况二:cur为parent的右:
如图:
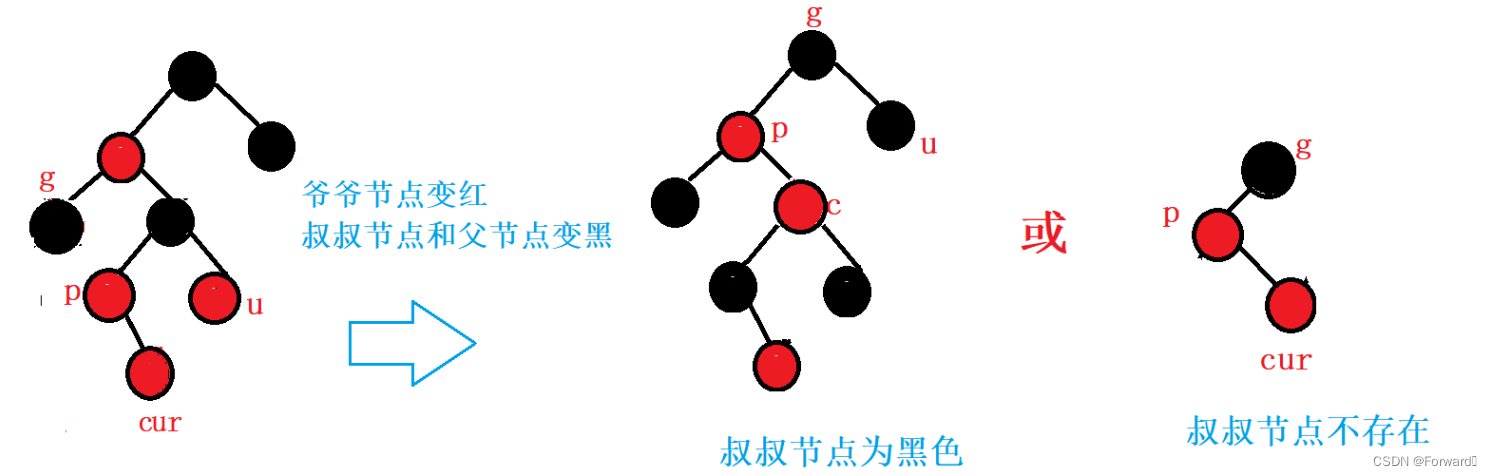
此时,我们需要对
grandparent进行左右双旋操作:
- 首先对
parent进行左单旋- 再对
grandparent进行右单旋
最后,调节节点的颜色,使其满足红黑树的条件:
cur的颜色变黑grandparent的颜色变红
对于叔叔节点不存在的情况,也执行相同的操作:
调整完毕
同样,假设这棵树是一棵树的子树,经过旋转调节过后也不会影响到其他点节点,可以直接结束插入过程
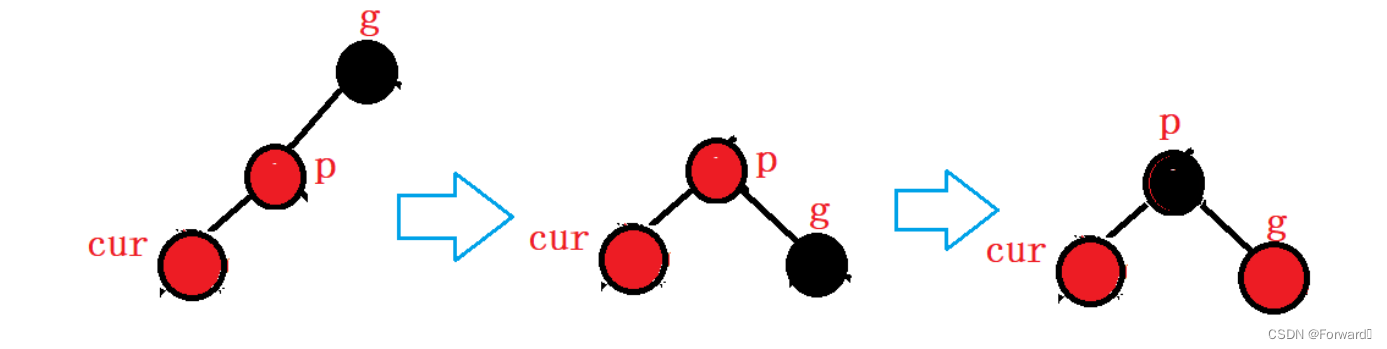
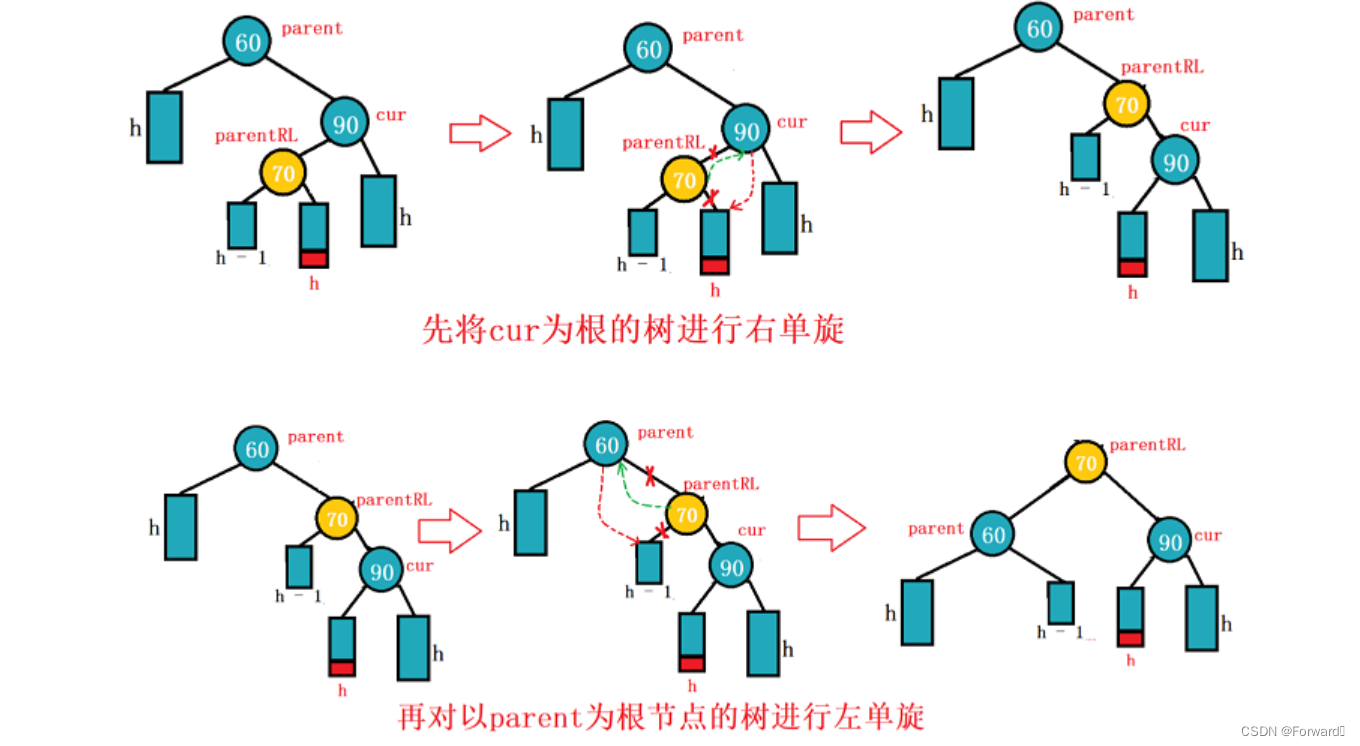
2.1.4.2.2 父节点parent为爷爷节点grandparent的右
情况一:cur为parent的右
如图:
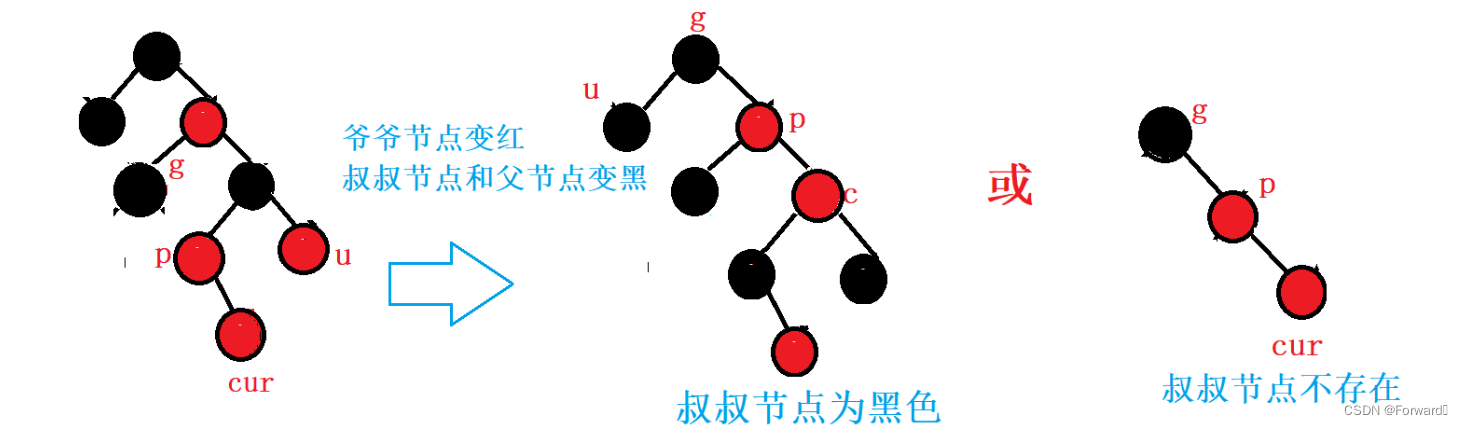
此时,我们需要对
grandparnet节点进行左单旋操作:
将
parent的左孩子链接给grandparent的右孩子将
grandparent链接给parent的左孩子
最后,调节节点的颜色,使其满足红黑树的条件:
grandparent的颜色红parnet的颜色变黑
对于叔叔节点不存在的情况,也执行相同的操作:
调整完毕
同样,假设这棵树是一棵树的子树,经过旋转调节过后也不会影响到其他点节点,可以直接结束插入过程
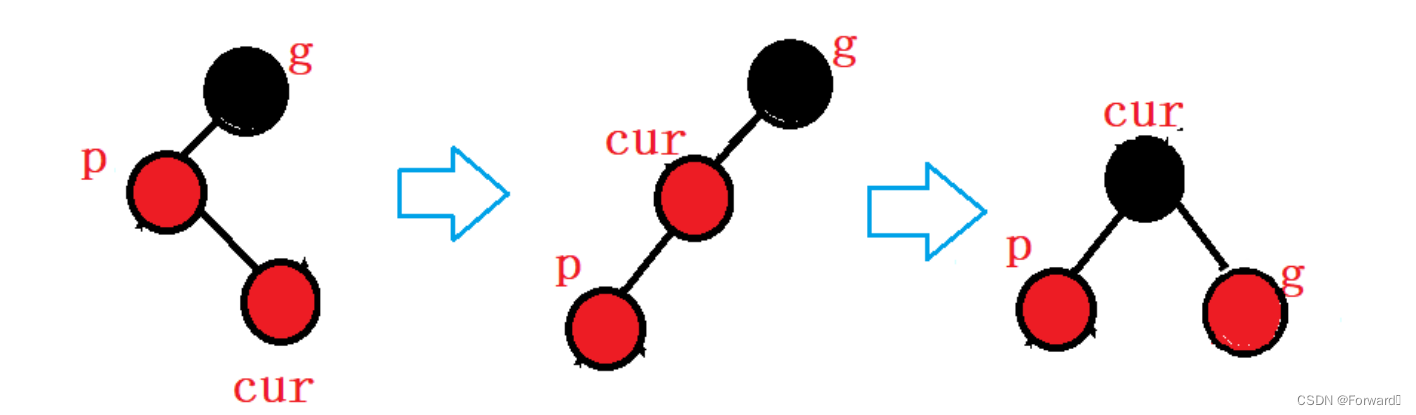
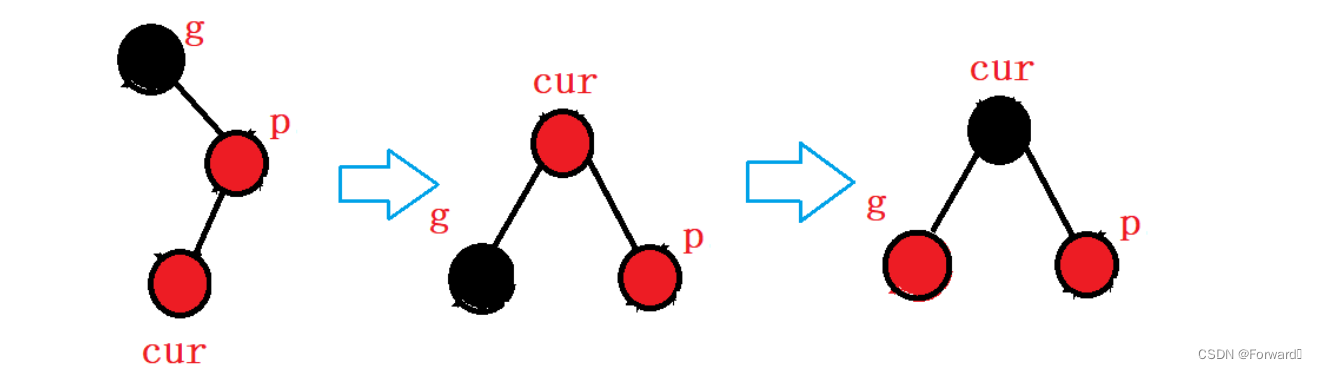
情况二:cur为parent的左:
如图:
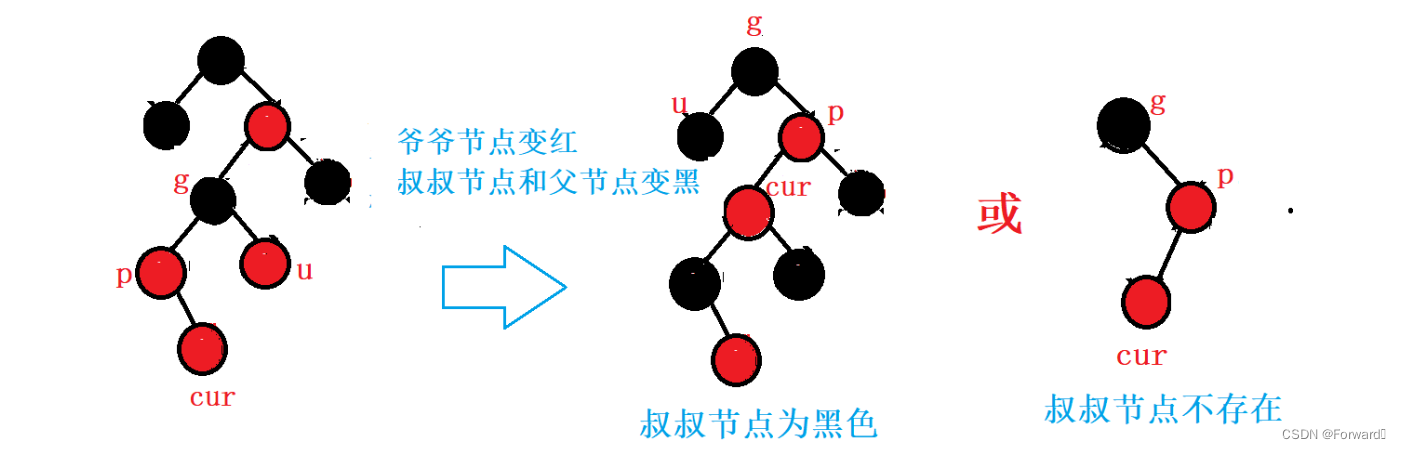
此时,我们需要对
grandparent进行右左双旋操作:
- 首先对
parent进行右单旋- 再对
grandparent进行左单旋
最后,调节节点的颜色,使其满足红黑树的条件:
cur的颜色变黑grandparent的颜色变红
对于叔叔节点不存在的情况,也执行相同的操作:
调整完毕
同样,假设这棵树是一棵树的子树,经过旋转调节过后也不会影响到其他点节点,可以直接结束插入过程
2.1.4.3 旋转操作
左单旋:
旋转步骤为:
cur的左子树链接给parent的右子树parent链接给cur的左子树
代码:
void rotateL(Node* parent) { Node* pparent = parent->_parent; Node* parentR = parent->_right; Node* parentRL = parentR->_left; parent->_right = parentRL; //考虑cur->_left为空的情况,防止空节点的访问 if (parentRL) parentRL->_parent = parent; parentR->_left = parent; parentR->_parent = pparent; parent->_parent = parentR; //如果cur就是_root根节点,那么就要更新根节点 if (pparent == nullptr) _root = parentR; else //否则就要将新的根(即cur)链接给上级节点 { if (parent == pparent->_left) pparent->_left = parentR; else pparent->_right = parentR; } }
右单旋:
旋转步骤为:
cur的右子树链接给parent的左子树parent链接给cur的右子树
代码:
void rotateR(Node* parent) { Node* pparent = parent->_parent; Node* parentL = parent->_left; Node* parentLR = parentL->_right; parent->_left = parentLR; //考虑cur->_right为空的情况 if (parentLR) parentLR->_parent = parent; parentL->_right = parent; parent->_parent = parentL; parentL->_parent = pparent; //如果cur就是_root根节点,那么就要更新根节点 if (pparent == nullptr) _root = parentL; else //否则就要将新的根(即cur)链接给上级节点 { if (parent == pparent->_left) pparent->_left = parentL; else pparent->_right = parentL; } }
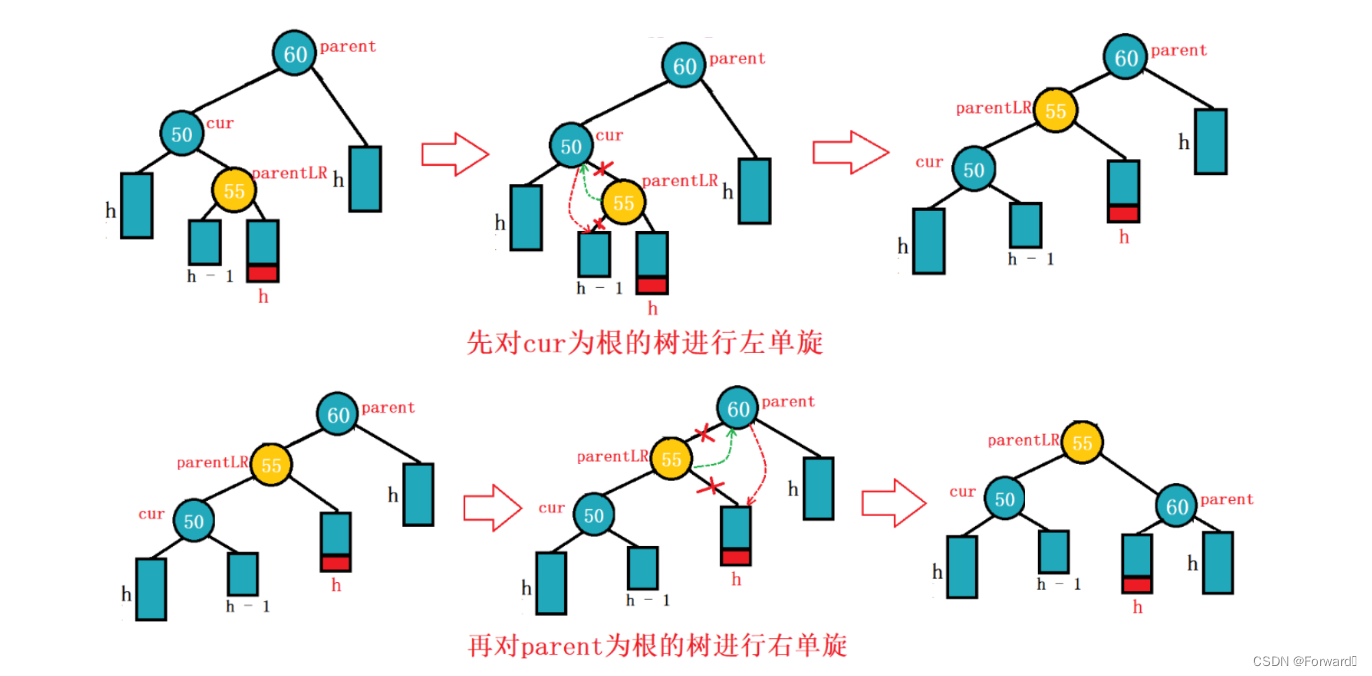
左右双旋:
旋转步骤为:
- 先对cur为根的树进行左单旋
- 再对parent为根的树进行右单旋
代码:
void rotateLR(Node* parent) { Node* parentL = parent->_left; //即图中的cur节点 Node* parentLR = parentL->_right; //即图中的parentLR节点 rotateL(parentL); //先对cur为根的树进行左单旋 rotateR(parent); //再对parent为根的树进行右单旋 }
右左双旋:
操作步骤为:
- 先对cur为根的树进行右单旋
- 再对parent为根的树进行左单旋
代码:
void rotateRL(Node* parent) { Node* parentR = parent->_right; //即为图中提到的cur节点 Node* parentRL = parentR->_left; //即为图中提到的parentRL节点 rotateR(parentR); //先对cur为根的树进行右单旋 rotateL(parent); //再对parent为根的树进行左单旋 }
2.1.5 插入节点代码
bool insert(const pair<K, V> kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_color = BLACK;
return true;
}
//找到插入位置
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
parent = cur;
if (cur->_kv.first > kv.first)
cur = cur->_left;
else if (cur->_kv.first < kv.first)
cur = cur->_right;
else
return false;
}
cur = new Node(kv);
cur->_parent = parent;
if (cur->_kv.first > parent->_kv.first)
parent->_right = cur;
else
parent->_left = cur;
//更新颜色,调节平衡
while (parent && parent->_color != BLACK)
{
Node* grandparent = parent->_parent;
//如果父节点为爷爷节点的左
if (parent == grandparent->_left)
{
Node* uncle = grandparent->_right;
//如果叔叔存在且叔叔节点为红色
if (uncle && uncle->_color == RED)
{
parent->_color = BLACK;
uncle->_color = BLACK;
grandparent->_color = RED;
//继续向上调整
cur = grandparent;
parent = grandparent->_parent;
}
else //如果叔叔节点不存在或叔叔节点为黑色
{
//如果cur为父节点的左,就进行右单旋
if (cur == parent->_left)
{
rotateR(grandparent);
grandparent->_color = RED;
parent->_color = BLACK;
}
else //如果cur为父节点的右,就进左右双旋
{
rotateLR(grandparent);
cur->_color = BLACK;
grandparent->_color = RED;
}
break; //旋转过后必定满足红黑树条件,直接结束插入
}
}
else //如果父节点为爷爷节点的右
{
Node* uncle = grandparent->_left;
//如果叔叔存在且叔叔节点为红色
if (uncle && uncle->_color == RED)
{
parent->_color = BLACK;
uncle->_color = BLACK;
grandparent->_color = RED;
//继续向上调整
cur = grandparent;
parent = grandparent->_parent;
}
else //如果叔叔节点不存在或叔叔节点为黑色
{
//如果cur为父节点的右,就进行左单旋
if (cur == parent->_right)
{
rotateL(grandparent);
grandparent->_color = RED;
parent->_color = BLACK;
}
else //如果cur为父节点的左,就进右左双旋
{
rotateRL(grandparent);
cur->_color = BLACK;
grandparent->_color = RED;
}
break; //旋转过后必定满足红黑树条件,直接结束插入
}
}
}
_root->_color = BLACK; //直接将根节点的颜色设置为黑色
return true;
}
2.3 检查一棵树是否为红黑树

为了验证我们的插入算法是否正确,我们需要写一个isbalance函数来进行检验:
我么可以根据红黑树的两个性质来实现这个函数;
红色节点不能重复出现
每条路径的黑色节点个数相同
对于第一个性质:
- 容易想到的一个方法是:递归遍历这棵树,每遍历到一个节点,就检查该节点是否和它的左孩子或者右孩子同时为红色
- 但是,上面的方法书写起来较为复杂。我们可以换一种思路:每遍历到一个节点,就检查它和它的父节点是否同时为红色
对于第二个性质:
- 我们需要求出每条路径的黑色节点的个数
- 而所谓路径,就是从根节点出发,到达空节点所经过的节点
- 因此,我们可以利用一个参数来记录遍历到当前节点时黑色节点的总个数
- 为了方便比较,我么可以预先求出一条路径的黑色节点总个数作为基准值
- 之后,当遍历到空节点时,就可以拿记录黑色节点个数的参数与基准值进行比较了
实现代码;
bool isBalance()
{
if (_root && _root->_color != BLACK)
return false;
//以最左路径的黑色节点纵作为基准值
int refBlackNum = 0;
Node* cur = _root;
while (cur)
{
if (cur->_color == BLACK)
refBlackNum++;
cur = cur->_left;
}
return cheak(_root, 0, refBlackNum);
}
bool cheak(Node* root, int curBlackNum, int refBlackNum)
{
//如果遍历到空节点就要拿curBlackNum与基准值refBlackNum进行比较
if (root == nullptr)
{
if (curBlackNum == refBlackNum)
return true;
else
{
cout << root->_kv.first << "改路径黑色节点的数量与最左路径黑色节点数量不同" << endl;
return false;
}
}
//如果当前节点和父节点同时为红色,则不满足红黑树条件
if (root->_color == RED && root->_parent->_color == RED)
{
cout << root->_kv.first << "存在连续的红色节点" << endl;
return false;
}
//如果当前节点为黑色,则当前路径的黑色节点个数加1
if (root->_color == BLACK)
curBlackNum++;
return cheak(root->_left, curBlackNum, refBlackNum) && cheak(root->_right, curBlackNum, refBlackNum);
}
2.4 AVL树与红黑树
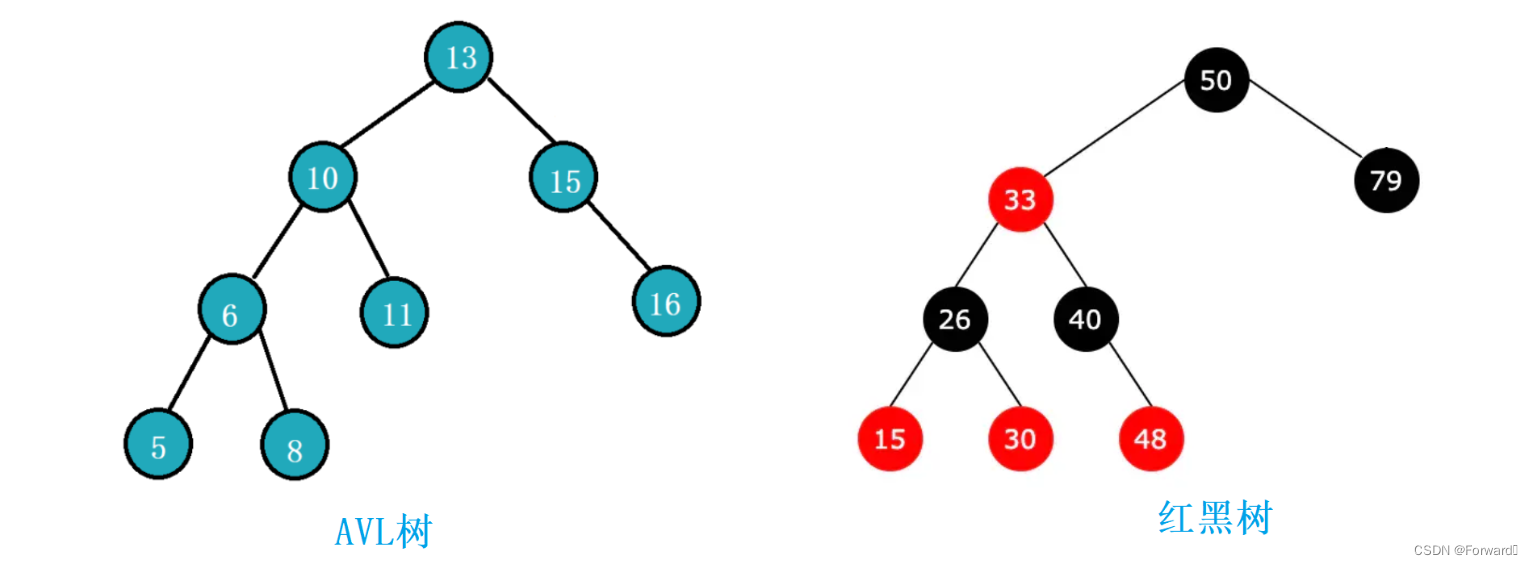
如今,我们已经学习了两颗自平衡的搜索二叉树:AVL树与红黑树
现在,我们来对二者进行一个简单的对比:
AVL树规定:每个节点的左右子树的高度差不大于1
红黑树的性质决定:最长路径的长度不大于最短路径的两倍
从上面的两个特性我们可以得出两个结论:
- AVL树的平衡条件比红黑树更加严格,因此AVL树也比红黑树更加平衡。就查找效率来说,AVL树是要比红黑树略高的。但是,由于二者都是平衡搜索二叉树,查找特定的元素的时间复杂度都是
O(logN)- 由于AVL树的平衡条件比红黑树要更加严格,因此维护其平衡也会更加复杂,同样是要删除或者插入一个元素,AVL树往往会比红黑树经历更多的旋转操作,这也就导致了在插入和删除元素的效率上,AVL树是不及红黑树的
可以做出总结:
- 如果需要频繁的查找树中的元素,而插入和删除元素的操作相对较少,可以优先使用AVL树
- 如果需要频繁的插入或删除元素,而查找元素的次数相对较少,可以优先使用红黑树
事实上,我们后面将学到的关联式容器map和set的底层结构就是红黑树

 菜鸟笔记
菜鸟笔记