八大排序算法及其优化

常见的排序算法

1. 直接插入排序

（1）算法基本思想

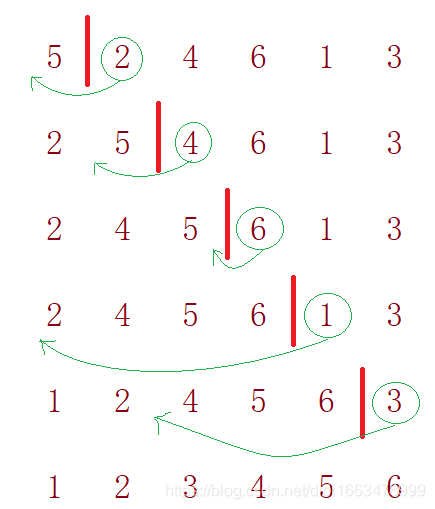
（2）特性总结：

1. 元素集合越接近有序，直接插入算法的时间效率越高
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)，它是一种稳定的排序算法
4. 稳定性：稳定

（3）代码实现：

void InsertSort(int* a, int n)
{ 
	for (int i = 0; i < n - 1; i++)
	{ 
		int end = i;
		int tmp = a[end + 1];
		while ()
		{ 
			if (tmp > a[end])
			{ 
				a[end + 1] = a[end];
				end--;

				a[end + 1] = tmp;
			}
			else
				break;
		}
	}
}

2. 希尔排序

（1）算法基本思想

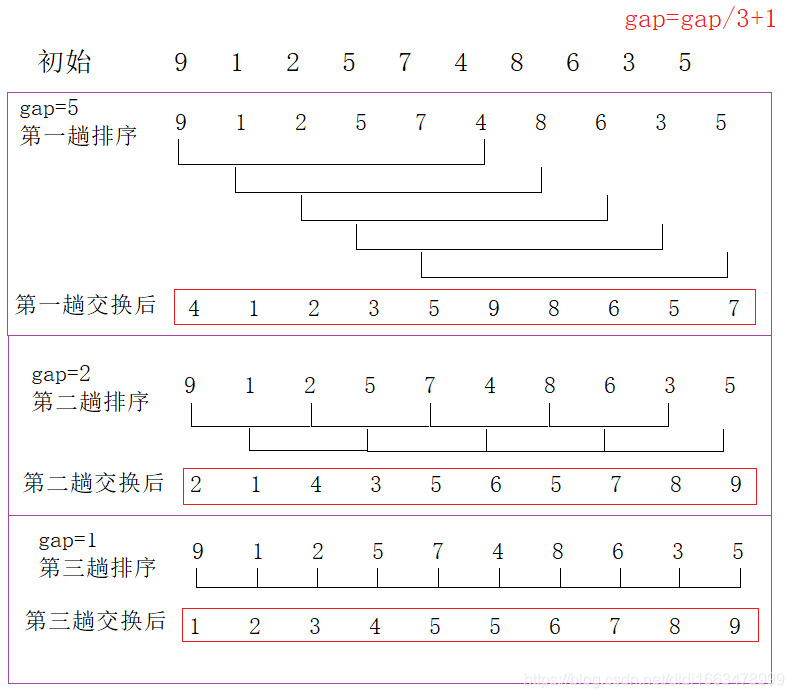
（2）特性总结：

1. 希尔排序是对直接插入排序的优化
2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序了，这样就会很快。这样整体而言，可以达到优化的效果。
3. 希尔排序的时间复杂度不好计算，需要进行推导，推导出来平均时间复杂度： O(N^1.3—N2）
4. 稳定性：不稳定

（3）代码实现：

void shellSort(int* a, int n)
{ 
	int gap = n;
	while (gap > 1)
	{ 
		gap = gap / 3 + 1;
		for (int i = 0; i < n - gap; i++)
		{ 
			if (a[i] > a[i + gap])
			{ 
				int tmp = a[i];
				a[i] = a[i + gap];
				a[i + gap] = tmp;
			}
		}
	}
}

3. 直接选择排序

（1）算法基本思想

（2）特性总结：

1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

（3）代码实现

void SelectSort(int* a, int n)
{ 
	int min = 0;
	int max = 0;
	
		for (int i = 0; i<n-1; i++)
		{ 
			min = i;
			
				for (int j = i; j < n-1; j++)
				{ 
					if (a[min] > a[j + 1])
					{ 
						min = j + 1;
					}
					
				}
				Swap(&a[min], &a[i]);
		}		
}

4. 堆排序

需要注意的是排升序要建大堆，排降序建小堆。

（1）算法基本思想

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了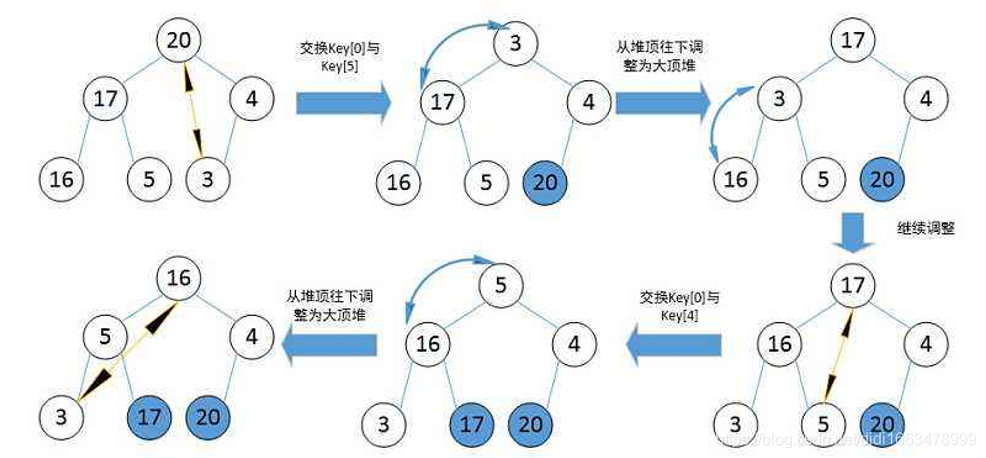
（2）特性总结

1. 堆排序使用堆来选数，效率就高了很多
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

（3）代码实现

void AjustDown(int* a, int root, int n)
{ 
	int parent = root;
	int child = parent * 2 + 1;
	while (child < n)
	{ 
		if (a[child] < a[child + 1] && child + 1 < n)
			++child;
		if (a[child] > a[parent])
		{ 
			int tmp = parent;
			parent = a[child];
			a[child] = tmp;

			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}
void HeapSort(int* a, int root, int n)
{ 
	//建大堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{ 
		AjustDown(a, i, n);
	}

	int end = n;
	for (int i = end; i >= 0; i--)
	{ 
		swap(a[0], a[end]);
		AjustDown(a, 0, i);
	}
}

5. 冒泡排序

（1）基本思想

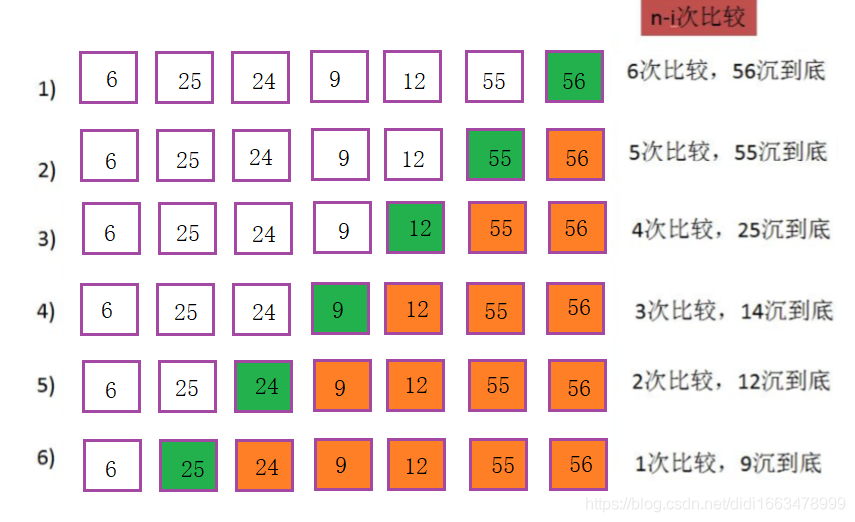
（2）特性总结

1. 冒泡排序是一种非常容易理解的排序
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：稳定

（3）代码实现

void BubbleSort(int* a, int n)
{ 
	int flag = 0;//优化
	for (int i = 0; i < n - 1; i++)
	{ 
		for (int j = 0; j < n - i; j++)
		{ 
			if (a[j] > a[j + 1])
			{ 
				swap(a[j], a[j+1]);
				flag = 1;
			}
		}
		if (flag == 0)
			break;
}

6. 快排

（1）基本思想

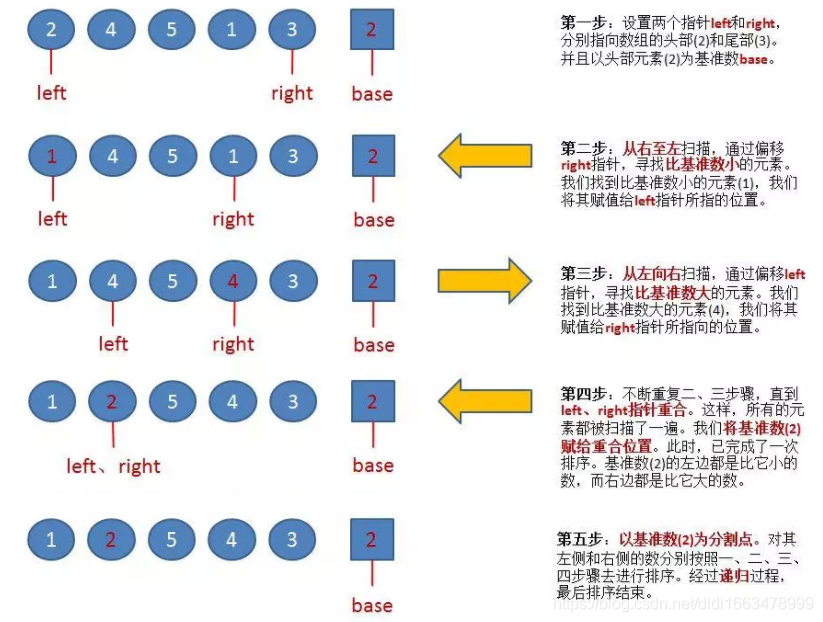
（2）特性总结

1. 快排整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(logN)
4. 稳定性：不稳定

（3）代码实现
代码1：

#include<stdio.h>
#include<stdlib.h>
int a[100], n;
void quicksort(int left, int right)
{ 
	int i;//指向第一个数
	int j;//指向最后一个数
	int tmp;//存基准数
	if (left > right)
		return;
	tmp = a[left];
	i = left;
	j = right;
	while (i != j)
	{ 
		while (i < j && a[j] >= tmp)
		{ 
			j--;
		}
		while (i < j && a[i] <= tmp)
		{ 
			i++;
		}
		if (i < j)
		{ 
			int t = a[i];
			a[i] = a[j];
			a[j] = t;
		}
	}
	//最终将基准数归位
	a[left] = a[i];
	a[i] = tmp;
	quicksort(left, i - 1);//继续处理左边的，这里是一个递归的过程
	quicksort(i + 1, right);//继续处理右边的 ，这里是一个递归的过程
}
int main()
{ 
	int i;
	//读入数据
	scanf("%d", &n);
	for (i = 1; i <= n; i++)
		scanf("%d", &a[i]);
	quicksort(1, n); //快速排序调用
	//输出排序后的结果
	for (i = 1; i < n; i++)
		printf("%d ", a[i]);

	system("pause");
	return 0;
}

代码2：

//这里还有一种简单的，通俗易懂的快速排序方法，代码如下：

#include <stdio.h>

void swap(int a[],int i,int j)
{ 
	int t;
	t=a[i];
	a[i]=a[j];
	a[j]=t;
}

void quickSort(int a[],int left,int right)
{ 
	int mid,i,j;

	if(left>=right)
		return;

	mid = a[left];
	i=left;
	j=left+1;
	while(j<=right)
	{ 
		if(a[j]<=mid)
		{ 
			i++;
			swap(a,i,j);
		}
		j++;
	}
	swap(a,i,left);
	quickSort(a,left,i-1);
	quickSort(a,i+1,right);
}

int main()
{ 
	int a[9]={ 8,2,6,12,1,9,5,5,10};
	int i;
	quickSort(a,0,8);/*排好序的结果*/
	for(i=0;i<9;i++)
	printf("%d\n",a[i]);
	return 0;
}

观察上面代码可知，j一直在向后移，而i只有在发生交换操作后才后移。可见，小于等于i坐标的数值都是小于等于mid值的，大于i坐标的数值都是大于mid值的。

i是先加1再交换的。

简单吧，通俗易懂吧，哈哈，希望对大家有帮助！

7. 归并排序

（1）基本思想

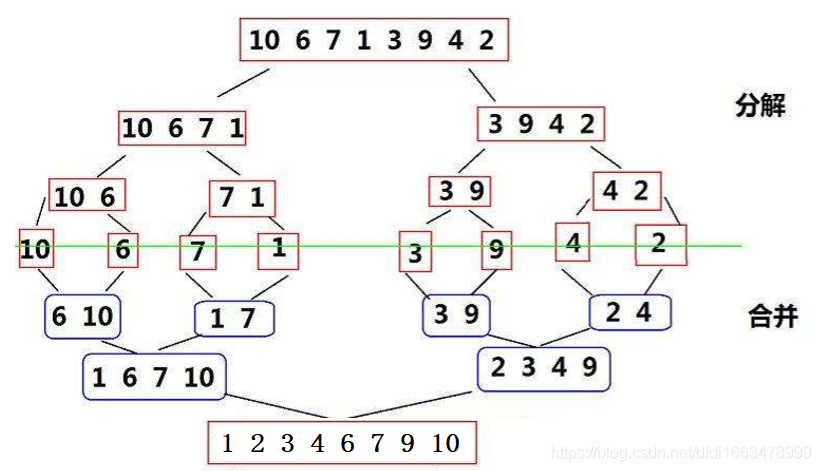
（2）特性总结

1. 归并排序的缺点在与需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排问题
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(N)
4. 稳定性：稳定

（3）代码实现

void _MergeSort(int* a, int left, int right, int* tmp)
{ 
	if (left >= left)
		return;
	//将它分为两部分
	int mid = left + ((right - left) >> 1);
	//[left, mid]
	//[mid+1, right]
	_MergeSort(a, left, mid, tmp);
	_MergeSort(a, mid + 1, right, tmp);

	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int index = left;

	while (begin1 <= end1 && begin2 <= end2)
	{ 
		if (a[begin1] < a[begin2])
			tmp[index++] = a[begin1++];
		else
			tmp[index++] = a[begin2++];
	}
	while (begin1 <= end1)
		tmp[index++] = a[begin1++];
	while (begin2 <= end2)
		tmp[index++] = a[begin2++];

	memcpy(a + left, tmp + left, sizeof(int)*(right - left + 1));
}