首先我们来看一个伪代码。这个是代表成绩的等级。
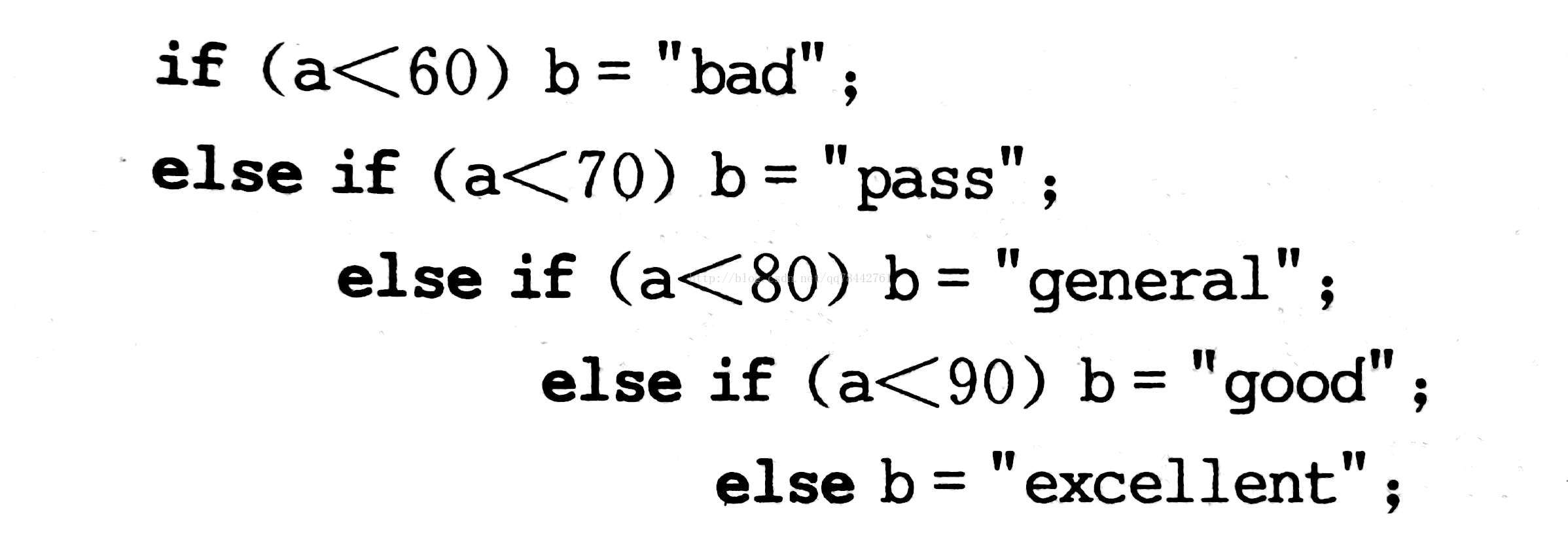
然后我们知道,每一次高考,学生的成绩分布应该接近某个比例,现在我们假如分别规律如下:

为此可以作出下面的这个树。
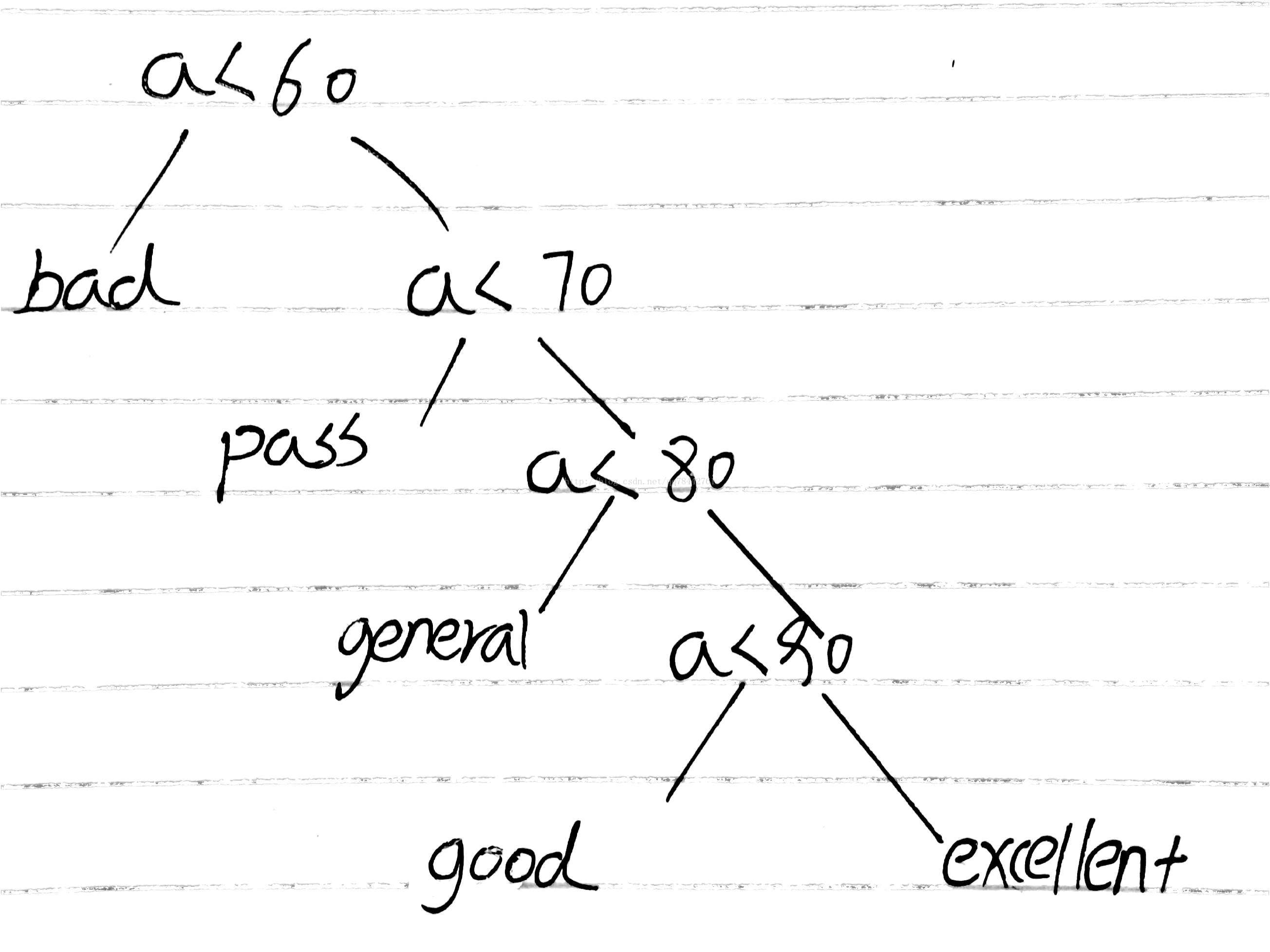
我们发现,概率分布主要是在70-79,80-89之间,如果有很多数据要比较,那么就要从60分开始比较,然后,分布最多的确是70-79,80-89的人,所以我们可以把树话成这样

现在先介绍几个概念:
路径长度:从树中一个结点到另一个结点之间的分支构成这两个结点的路径,路径上的分支数目叫路径长度。
树的路径长度:根结点到每个结点的路径长度和。
WPL(weight path length):树中所有叶子结点的带权路径之和。
比如上面那两个图,我们把他权重标号。如下图所示(为了方便,我们扩大10倍,避免小数点)
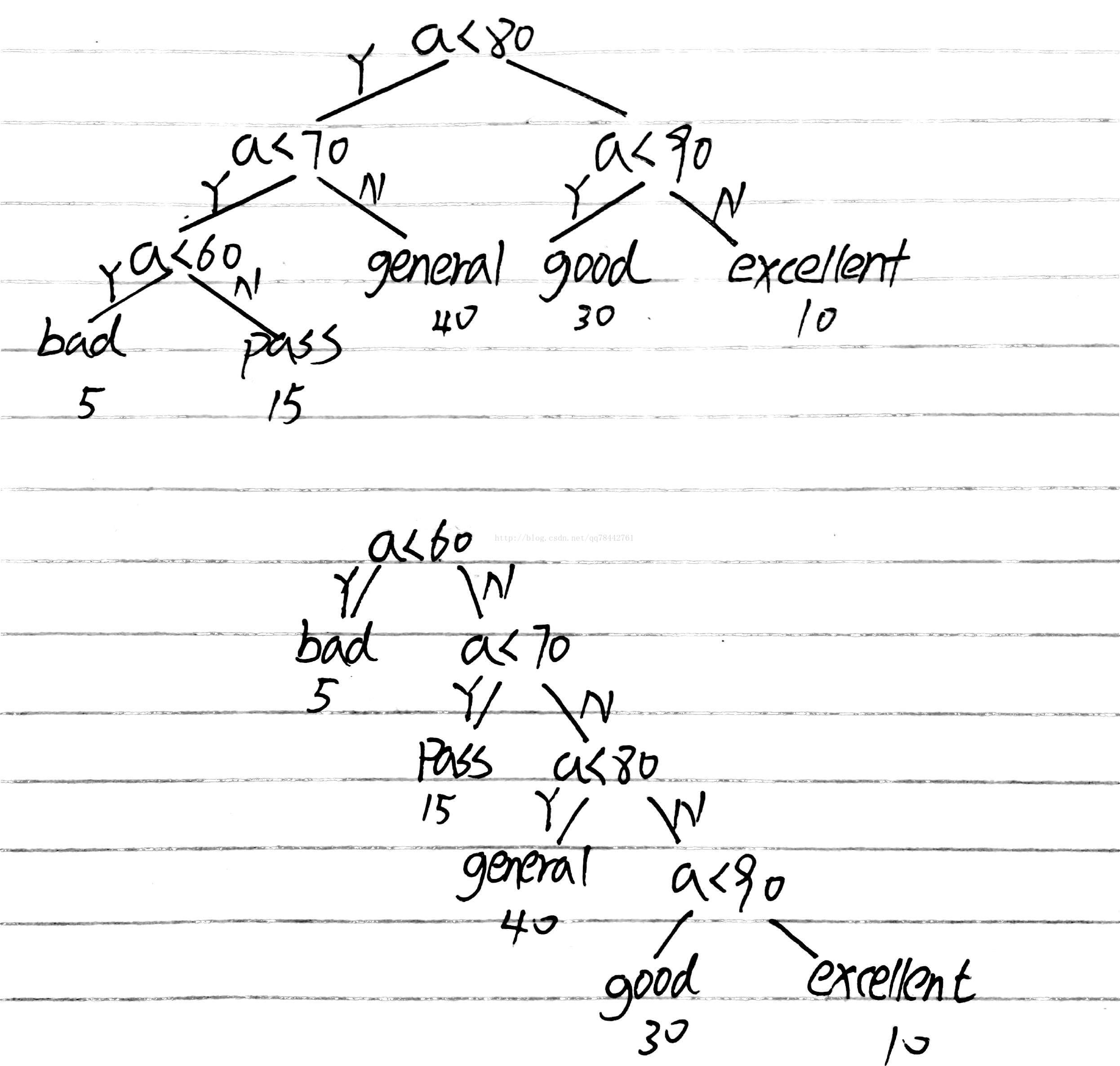
现在来看看WPL
WPL1=5*3+15*3+40*2+30*2+10*2=220
WPL2=5*1+15*+40*3+30*4+10*4=315。
现在给出一个概念:带权路径长度WPL最小的二叉树叫最优二叉树或赫夫曼树。
下面给出最优二叉树或赫夫曼树的画法。
规则如下:
1.在森林中选出两颗根结点的权值最小的二叉树。
2.合并两颗,增加一个新结点作为新二叉树的根,全职为左右孩子的权重之和。
3.再从未选中的结点中选择,小的放左边,大的放右边,然后重复,一直到结点没有了为止。
如下图所示:
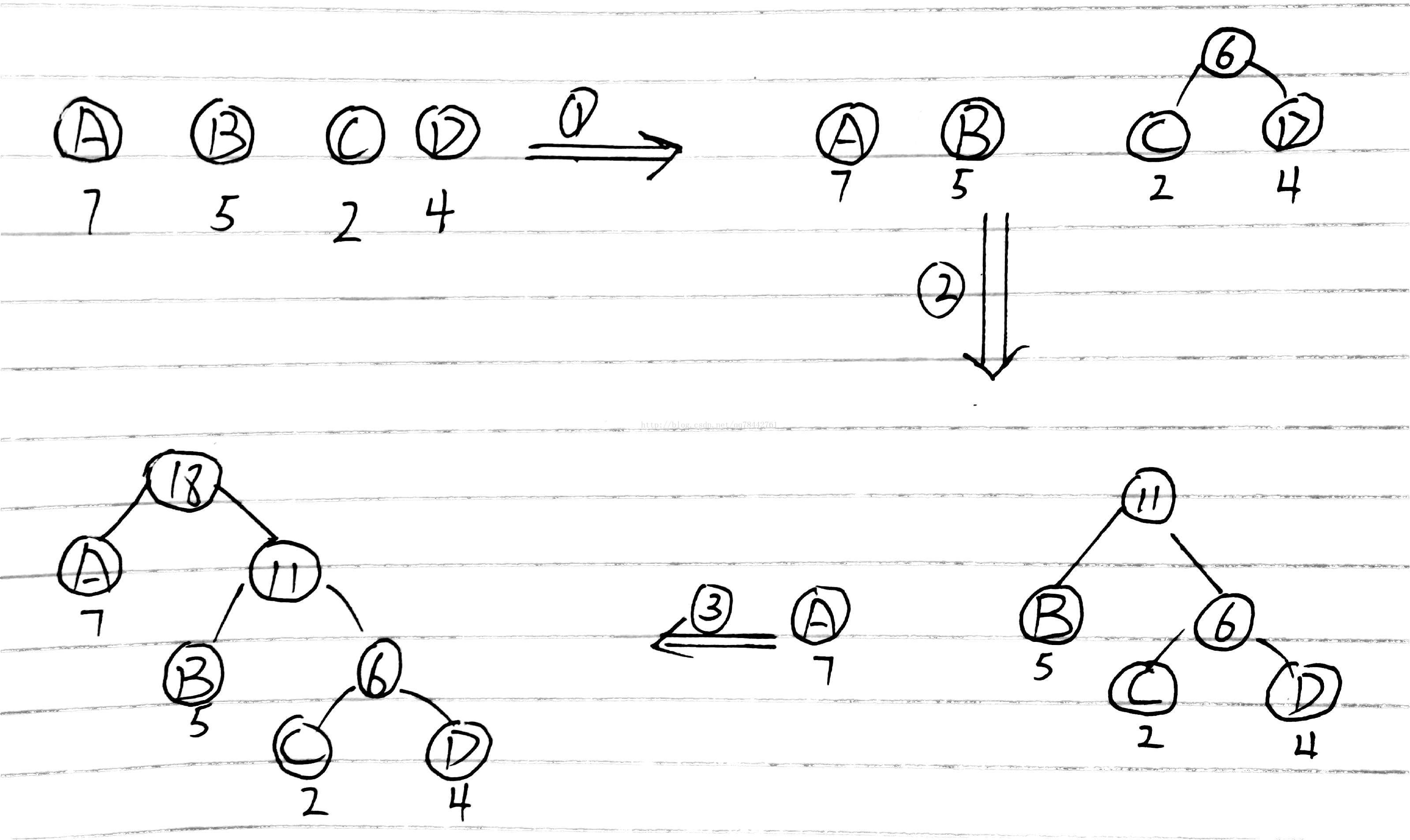

 菜鸟笔记
菜鸟笔记