一. 算法描述
希尔排序:将无序数组分割为若干个子序列,子序列不是逐段分割的,而是相隔特定的增量的子序列,对各个子序列进行插入排序;然后再选择一个更小的增量,再将数组分割为多个子序列进行排序……最后选择增量为1,即使用直接插入排序,使最终数组成为有序。
增量的选择:在每趟的排序过程都有一个增量,至少满足一个规则 增量关系 d[1] > d[2] > d[3] >..> d[t] = 1 (t趟排序);根据增量序列的选取其时间复杂度也会有变化,这个不少论文进行了研究,在此处就不再深究;本文采用首选增量为n/2,以此递推,每次增量为原先的1/2,直到增量为1;
为方便理解我还准备了动图:
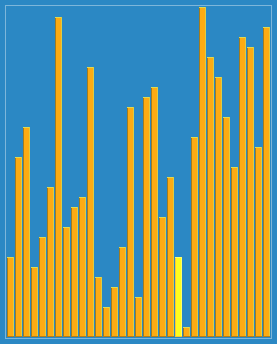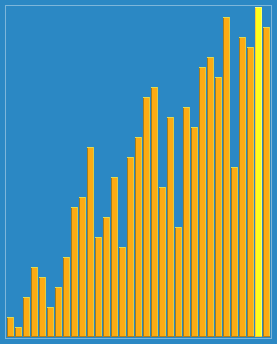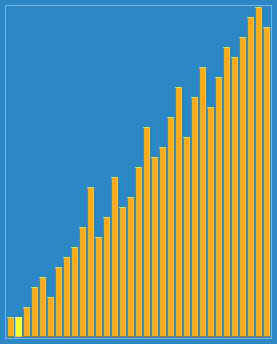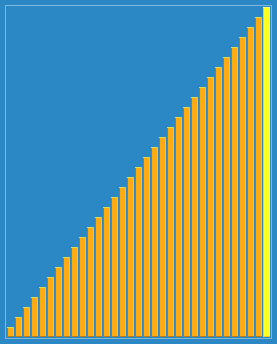
二. 算法分析
平均时间复杂度:希尔排序的时间复杂度和其增量序列有关系,这涉及到数学上尚未解决的难题;不过在某些序列中复杂度可以为O(n1.3);
空间复杂度:O(1)
稳定性:不稳定
三. 算法实现
//交换数组元素
void swap(int *a,int i,int j)
{
int t = a[i];
a[i] = a[j];
a[j] = t;
}
//希尔排序
void shell_sort(int *a,int len)
{
int h=1,i,j;
while(h<len/3) //寻找合适的间隔h
{
h = 3*h+1;
}
while(h>=1)
{
//将数组变为间隔h个元素有序
for (i = h; i < len; i++)
{
//间隔h插入排序
for (j = i; j >= h && a[j] < a[j-h]; j -= h)
{
swap(a, j, j-h);
}
}
h /= 3;
}
}

 菜鸟笔记
菜鸟笔记