文章目录
- 什么是方差(Variance)
-
- 方差公式的含义(为什么方差公式长这个样子)
- 总体方差
- 样本方差
-
- 为什么样本偏差要是n-1
- 什么是标准差(Standard Deviation)
- 什么是相对标准偏差(Relative Standard Deviation)
- 什么是正态分布(Normal Distribution)
-
- 正态分布的性质
- 参考文献
什么是方差(Variance)
方差描述了一组数据距离他们平均值的离散程度。(Variance measures the dispersion of a set of data points around their mean)
例如,如果一个班的平均分是50分,可能有两种极端情况:
- 大部分人都在50左右附近徘徊:这种情况,说明数据集的每个数据距离平局值较近,离散程度小,方差较小
- 一半人接近一百分,另一半人接近0分:这种情况说明数据集的每个数据距离平局值较远,离散程度大,方差较大
这样,我们就可以通过对比两个班的方差,来计算哪个班的成绩比较稳定。
方差分为两种:
- 样本方差(Sample Variance):样本方差只选取整体数据的一部人来计算。当我们很难获取到整体数据时,就可以使用样本方差。公式如下: S 2 = ∑ i = 1 n ( x i − x ˉ ) 2 n − 1 S^2 = \frac{\sum^{n}_{i=1} (x_i-\bar{x})^2}{n-1} S2=n−1∑i=1n(xi−xˉ)2
- 总体方差(Population Variance):使用所有数据来计算方差。公式如下: σ 2 = ∑ i = 1 N ( x i − μ ) 2 N \sigma^2 = \frac{\sum_{i=1}^{N} (x_i -\mu)^2}{N} σ2=N∑i=1N(xi−μ)2
总体方差的符号为 σ 2 \sigma^2 σ2,样本方差的符号为 S 2 S^2 S2
方差公式的含义(为什么方差公式长这个样子)
我们把重点放在分子上: ∑ i = 1 n ( x i − x ˉ ) 2 \sum^{n}_{i=1} (x_i-\bar{x})^2 ∑i=1n(xi−xˉ)2
x i − x ˉ x_i-\bar{x} xi−xˉ : 距离平均值越小的数据,该结果越小,距离平均值越大的数据,该值越大。
那为什么又要加一个平方呢? ( x i − x ˉ ) 2 (x_i-\bar{x})^2 (xi−xˉ)2,主要有两个目的:
- 消除负数:如果不平方的话就会有负值存在,这样一求和,正负抵消了。
- 放大远距离数据的影响力:平方嘛,数据越大,平方后的结果就越大,这样可以更好的描述数据的离散程度
总体方差
总体方差公式如下:
σ 2 = ∑ i = 1 N ( x i − μ ) 2 N \sigma^2 = \frac{\sum_{i=1}^{N} (x_i -\mu)^2}{N} σ2=N∑i=1N(xi−μ)2
其中, μ \mu μ 为总体数据的平均值, N N N 为总数, x i x_i xi 为每个数据的值
样本方差
样本方差的公式如下:
S 2 = ∑ i = 1 n ( x i − x ˉ ) 2 n − 1 S^2 = \frac{\sum^{n}_{i=1} (x_i-\bar{x})^2}{n-1} S2=n−1∑i=1n(xi−xˉ)2
其中, x ˉ \bar{x} xˉ 为样本数据的平均值, n n n 为样本的总数, x i x_i xi 为每个数据的值
为什么样本偏差要是n-1
简单来说,如果不减1的话,那么样本方差一定小于总体方差。
数学证明如下(假设样本方差不减1):
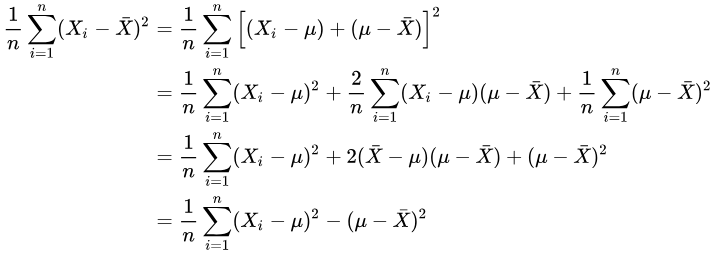
由上式子可以看出,除非当 X ˉ = μ \bar{X}=\mu Xˉ=μ 时,否则一定有
而在实践中,我们无法得知总体数据的平均值,所以就通过对 n − 1 n-1 n−1 的方式将样本方差稍微增大,以减少与实际方差的误差。
补充,上述式子,稍有难理解的地方:
2 n ∑ i = 1 n ( X i − μ ) = 2 n ( ( X 1 − μ ) + ( X 2 − μ ) + ⋯ + ( X n − μ ) ) = 2 ( X 1 + X 2 + ⋯ + X n ) n − 2 n ∗ n ∗ μ = 2 X ˉ − 2 μ = 2 ( X ˉ − μ ) \begin{aligned} \frac{2}{n} \sum^{n}_{i=1}(X_i – \mu) = & \frac{2}{n} ((X_1 – \mu) + (X_2 – \mu) + \cdots + (X_n – \mu)) \\\\ = & 2\frac{(X_1 + X_2 +\cdots + X_n)}{n} – \frac{2}{n} * n* \mu \\ \\ = & 2\bar{X} – 2\mu \\ \\ = & 2(\bar{X} – \mu) \end{aligned} n2i=1∑n(Xi−μ)====n2((X1−μ)+(X2−μ)+⋯+(Xn−μ))2n(X1+X2+⋯+Xn)−n2∗n∗μ2Xˉ−2μ2(Xˉ−μ)
什么是标准差(Standard Deviation)
学过数学的都知道,把方差开平方就是标准差。
- 总体标准差:符号 σ \sigma σ, σ = σ 2 \sigma = \sqrt{\sigma^2} σ=σ2
- 样本标准差:符号 S S S, S = S 2 S = \sqrt{S^2} S=S2
那么为什么有了方差,还要引入标准差呢,或者说,为什么开了方,就是标准差呢?
其实,这是为了保证使数据的量纲保持一致。举例来说:
一个班的平局身高为170cm。该班身高的标准差为10cm,方差为100cm
从这个例子就可以看出,通过标准差,我们我可以看出,该班学生的身高大概围绕着170cm上下10cm进行浮动。但是看方差却看不出个所以然
什么是相对标准偏差(Relative Standard Deviation)
相对标准偏差(Relative Standard Deviation)也可以称为相对标准差,变异系数,标准偏差系数(Coefficient of Variation,CV)。
有了标准差了,为什么又要搞一个相对标准偏差呢?
来看下面这个例子:
假设一个汉堡在美国的不同地区的价格不一样,分别为:1,2,3,4,5,6,7,8,9,10
若现在的美元兑中国的汇率是1:6,那么使用RMB买,价格为:6,12,18,24,30,36,42,48,54,60
那么根据这两个数据,我们很容易得到两组数据:
| 地区 | 平均值 | 方差 | 标准差 |
|---|---|---|---|
| 美国 | 5.5 | 8.25 | 2.87228 |
| 中国 | 33 | 297 | 17.23369 |
此时,你拿着这组数据说,RMB买买汉堡时,离散程度(波动程度)要远大于美元。这显然是不合适的。 所以此时,为了针对单位不一致时可以更准确的说明两组数据的离散程度,就引入了相对标准偏差。计算公式也很简单,只需要用标准差除以平均值就是相对标准偏差
- 总体相对标准偏差: C V = σ μ CV=\frac{\sigma}{\mu} CV=μσ
- 样本相对标准偏差: C V = S x ˉ CV=\frac{S}{\bar{x}} CV=xˉS
此时,我们再对上述两组数据进行比较:
| 地区 | 平均值 | 方差 | 标准差 | 相对标准偏差 |
|---|---|---|---|---|
| 美国 | 5.5 | 8.25 | 2.87228 | 2.87228 / 5.5 = 0.522 |
| 中国 | 33 | 297 | 17.23369 | 17.23369 / 33 = 0.522 |
通过对比相对标准偏差,我们可以看到,其实这两组数据的离散程度是一致的
什么是正态分布(Normal Distribution)
讨论完上面的,就可以开始说正态分布了。
正态分布,英文为Normal Distribution,顾名思义:正常的分布。
生活中大部分数据分布并不是均匀的,例如:收入水平、考试成绩。这些数据都有一个特征:中间数据量多,两边数据量少。最终形成如下图所示的分布情况:

如果实际举例,横坐标为工资,那纵坐标就是人数。中间的 μ \mu μ 为平均工资。
正态分布函数图像的方程式如下:
f ( x ) = 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 ) f(x) = \frac{1}{\sqrt{2\pi} \sigma} \exp(-\frac{(x-\mu)^2}{2\sigma^2}) f(x)=2π σ1exp(−2σ2(x−μ)2)
该公式中,包含一个自变量 x x x,两个常量 μ \mu μ 和 σ \sigma σ ,其中 μ \mu μ 是指总体平均值, σ \sigma σ是标准差。该公式记做:
X ∼ N ( μ , σ 2 ) X \sim N (\mu, \sigma^2) X∼N(μ,σ2)
读作X服从正态分布。
正态分布的性质
我们根据下图这个例子:
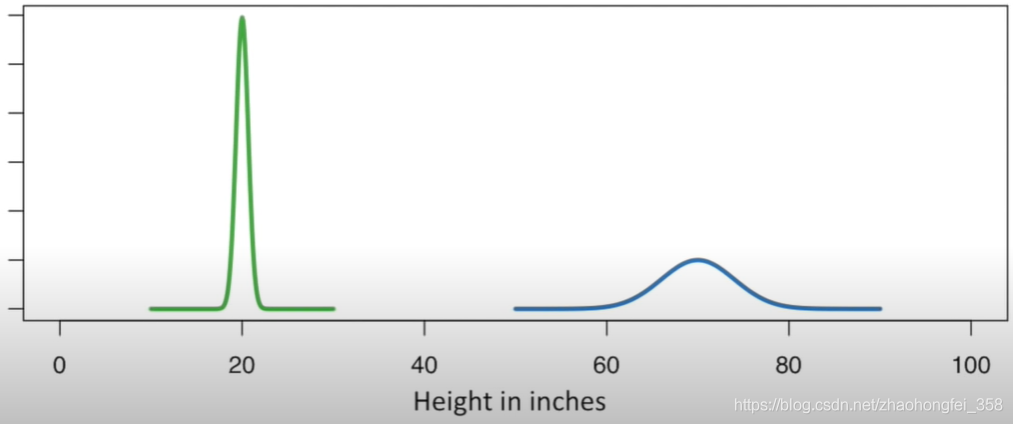
绿色的线表示婴儿出生时的身高(单位英尺)分布,蓝色的线表示成人的身高分布。这两个数据都符合正态分布。
其中可以看出,绿色的平均值 20,即 μ 绿 = 20 \mu_绿 = 20 μ绿=20,而蓝色的平均值是70,即 μ 蓝 = 70 \mu_蓝=70 μ蓝=70。
所以,正态分布中的平均值 μ \mu μ 是用来决定图的中线在哪里
除此之外可以看出,绿色线的波动范围大概为 ± 5 \pm 5 ±5 英尺,即标准差为5英尺 σ 绿 = 5 \sigma_绿=5 σ绿=5,蓝色线的波动范围大概是 ± 10 \pm 10 ±10英尺,即标准差为10英尺 σ 蓝 = 10 \sigma_蓝=10 σ蓝=10。
所以,正态分布的宽窄,是由标准差决定的
再看,绿色线波动范围要小,所婴儿出生身高为20英尺的概率很大,而蓝色波动范围大,所以一个成年人身高为70英尺的概率相对就会小。所以蓝色线的高度远低于绿色线
所以,正态分布的标准差越小,这个图像就会越高,标准差越大,就会越矮
那么,另一个问题来了,有多少成年人是在 170 ± 10 170\pm10 170±10上下浮动呢,可以通过该图进行说明:
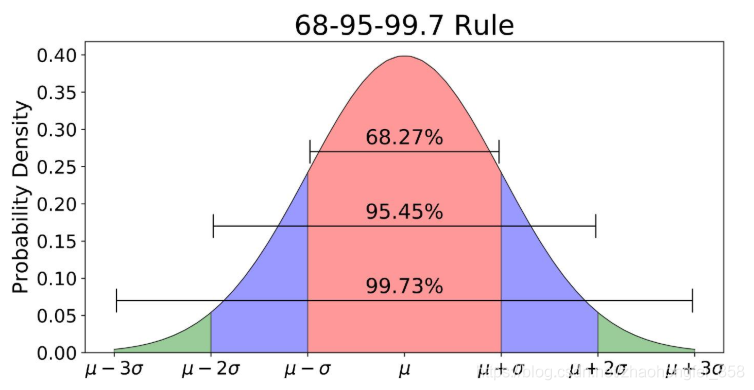
从图中可以看出,正态分布的主要三块面积为:
- 68.27% 的数据落在 u ± σ u\pm\sigma u±σ的区间上
- 95.45% 的数据落在 u ± 2 σ u\pm2\sigma u±2σ的区间上
- 99.73% 的数据落在 u ± 3 σ u\pm3\sigma u±3σ的区间上
这个规则适用于所有的正态分布

 菜鸟笔记
菜鸟笔记