粒子滤波理论

粒子滤波通过非参数化的蒙特卡洛 (Monte Carlo) 模拟方法来实现递推贝叶斯滤波，适用于任何能用状态空间模型描述的非线性系统，精度可以逼近最优估计。粒子滤波器具有简单、易于实现等特点，它为分析非线性动态系统提供了一种有效的解决方法，从而引起目标跟踪、信号处理以及自动控制等领域的广泛关注。首先概述用于求解目标状态后验概率的贝叶斯滤波理论随后介绍具有普遍适用性的粒子滤波器，最后针对当前粒子滤波器存在的粒子多样性丧失问题，提出了一种量子进化粒子滤波算法。

贝叶斯滤波

动态系统的目标跟踪问题可以通过图所示的状态空间模型来描述。本节在贝叶斯滤波框架下讨论目标跟踪问题。

其中 f(), h() 分别为状态转移方程与观测方程，在目标跟踪问题中，动态系统的状态空间模型可描述为
x k = f ( x k − 1 ) + u k − 1 x_k=f(x_{k-1})+u_{k-1} xk=f(xk−1)+uk−1
y k = h ( x k ) + v k y_k=h(x_k)+v_k yk=h(xk)+vk
为了描述方便，用 X k = x 0 : k X_k=x_{0:k} Xk=x0:k={ x 0 , x 1 , . . . , x k x_0,x_1,...,x_k x0,x1,...,xk}与 Y k = y 0 : k Y_k=y_{0:k} Yk=y0:k={ y 0 , y 1 , . . . , y k y_0,y_1,...,y_k y0,y1,...,yk}分别表示 0 到 k 时刻所有的状态与观测值。

在处理目标跟踪问题时，通常假设目标的状态转移过程服从一阶马尔可夫模型：

假设当前时刻的状态 x k x_k xk 只与上一时刻的状 x k − 1 x_{k-1} xk−1有关
假设观测值相互独立，即观测值 y k y_k yk只与 k 时刻的状态 x k x_k xk有关

贝叶斯滤波为非线性系统的状态估计问题提供了一种基于概率分布形式的解决方案。贝叶斯滤波将状态估计视为一个概率推理过程，即将目标状态的估计问题转换为利用贝叶斯公式求解后验概率密度 p ( x k ∣ Y k ) p(x_k|Y_k) p(xk∣Yk) 或滤波概率密度 p ( x k ∣ Y k ) p(x_k|Y_k) p(xk∣Yk)，进而获得目标状态的最优估计。
贝叶斯滤波包含预测和更新两个阶段：

预测过程：利用系统模型预测状态的先验概率密度
更新过程：利用最新的测量值对先验概率密度进行修正，得到后验概率密度

假设已知 k 1 k_1 k1 时刻的概率密度函数为 p ( x k − 1 ∣ Y k − 1 ) p(x_{k-1}|Y_{k-1}) p(xk−1∣Yk−1)，贝叶斯滤波的具体过程如下：

预测过程，由 p ( x k − 1 ∣ Y k − 1 ) p(x_{k-1}|Y_{k-1}) p(xk−1∣Yk−1)得到 p ( x k ∣ Y k − 1 ) p(x_{k}|Y_{k-1}) p(xk∣Yk−1)
p ( x k , x k − 1 ∣ Y k − 1 ) = p ( x k ∣ x k − 1 , Y k − 1 ) p ( x k − 1 ∣ Y k − 1 ) p(x_k,x_{k-1}|Y_{k-1})=p(x_k|x_{k-1},Y_{k-1}) p(x_{k-1}|Y_{k-1}) p(xk,xk−1∣Yk−1)=p(xk∣xk−1,Yk−1)p(xk−1∣Yk−1)

当给定 x k − 1 x_{k-1} xk−1时，状态 x k x_k xk与 Y k − 1 Y_{k-1} Yk−1相互独立，所以：
p ( x k , x k − 1 ∣ Y k − 1 ) = p ( x k ∣ x k − 1 ) p ( x k − 1 ∣ Y k − 1 ) p(x_k,x_{k-1}|Y_{k-1})=p(x_k|x_{k-1})p(x_{k-1}|Y_{k-1}) p(xk,xk−1∣Yk−1)=p(xk∣xk−1)p(xk−1∣Yk−1)
对上式 x k − 1 x_{k-1} xk−1积分：
p ( x k , ∣ Y k − 1 ) = ∫ p ( x k ∣ x k − 1 ) p ( x k − 1 ∣ Y k − 1 ) d x k − 1 p(x_k,|Y_{k-1})=\int p(x_k|x_{k-1})p(x_{k-1}|Y_{k-1})dx_{k-1} p(xk,∣Yk−1)=∫p(xk∣xk−1)p(xk−1∣Yk−1)dxk−1

跟新过程，由 p ( x k , ∣ Y k − 1 ) p(x_k,|Y_{k-1}) p(xk,∣Yk−1)得到 p ( x k , ∣ Y k ) p(x_k,|Y_{k}) p(xk,∣Yk)：
获取 k 时刻的测量 y k y_k yk后，利用贝叶斯公式对先验概率密度进行更新，得到后验概率

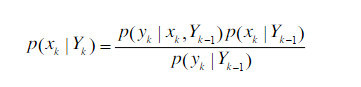
假设 y k y_k yk只有 x k x_k xk决定，即：
p ( y k ∣ x k , Y k − 1 ) = p ( y k ∣ x k ) p(y_k|x_k,Y_{k-1})=p(y_k|x_k) p(yk∣xk,Yk−1)=p(yk∣xk)
因此：

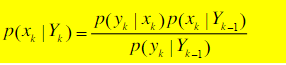
其中， p ( y k ∣ Y k − 1 ) p(y_k|Y_{k-1}) p(yk∣Yk−1)为归一化常数

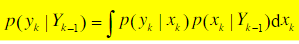
贝叶斯滤波以递推的形式给出后验 (或滤波 )概率密度函数的最优解。目标状态的最优估计值可由后验 ( 或滤波 ) 概率密度函数进行计算。通常根据极大后验 (MAP) 准则或最小均方误差(MMSE) 准则，将具有极大后验概率密度的状态或条件均值作为系统状态的估计值，即
x ^ k M A P = a r g m i n p ( x k ∣ Y k ) \hat{x}_k^{MAP}=argminp(x_k|Y_k) x^kMAP=argminp(xk∣Yk)
x ^ k M M S E = ∫ E ( [ x k ∣ Y k ] ) = ∫ f ( x k ) p ( x k ∣ Y k ) d x k \hat{x}_k^{MMSE}=\int E([x_k|Y_k])=\int f(x_k)p(x_k|Y_k)dx_k x^kMMSE=∫E([xk∣Yk])=∫f(xk)p(xk∣Yk)dxk
贝叶斯滤波需要进行积分运算，除了一些特殊的系统模型（如线性高斯系统，有限状态的离散系统）之外，对于一般的非线性、非高斯系统，贝叶斯滤波很难得到后验概率的封闭解析式。因此，现有的非线性滤波器多采用近似的计算方法解决积分问题，以此来获取估计的次优解。在系统的非线性模型可由在当前状态展开的线性模型有限近似的前提下，基于一阶或二阶Taylor级数展开的扩展Kalman滤波得到广泛应用。在一般情况下，逼近概率密度函数比逼近非线性函数容易实现。据此，Julier与Uhlmann提出一种Unscented Kalman滤波器，通过选定的sigma点来精确估计随机变量经非线性变换后的均值和方差，从而更好的近似状态的概率密度函数，其理论估计精度优于扩展Kalman滤波。获取次优解的另外一中方案便是基于蒙特卡洛模拟的粒子滤波器。
## 粒子滤波
标准的粒子滤波算法流程为：

贝叶斯重要性采样

粒子滤波算法的核心思想便是利用一系列随机样本的加权和表示后验概率密度，通过求和来近似积分操作。假设可以从后验概率密度 p ( x k , Y k ) p(x_k,Y_k) p(xk,Yk)中抽取N个独立同分布的随机样本 x k ( i ) , i = 1 , . . . , N x_k^{(i)},i=1,...,N xk(i),i=1,...,N，则有

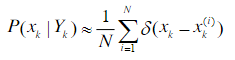
这里 x k x_k xk为连续变量， δ ( x − x k ) \delta (x-x_k) δ(x−xk)为单位冲激函数(狄拉克函数)，即 δ ( x − x k ) = 0 \delta (x-x_k)=0 δ(x−xk)=0， x ≠ x k x \neq x_k x=xk,且 ∫ δ ( x ) d x = 1 \int \delta (x)dx=1 ∫δ(x)dx=1.

当 x k x_k xk为离散变量时，后验概率分布 P ( x k ∣ Y k ) P(x_k|Y_k) P(xk∣Yk)可近似逼近为:

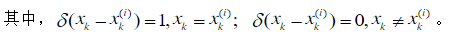
设 x k ( i ) x_k^{(i)} xk(i)为从后验概率密度函数 p ( x k ∣ Y k ) p(x_k|Y_k) p(xk∣Yk)中获取的采样粒子，则任意函数 f ( x k ) f(x_k) f(xk) 的期望
估计可以用求和方式逼近，即

蒙特卡洛方法一般可以归纳为以下三个步骤：

构造概率模型。对于本身具有随机性质的问题，主要工作是正确地描述和模拟这个概率过程。对于确定性问题，比如计算定积分、求解线性方程组、偏微分方程等问题，采用蒙特卡洛方法求解需要事先构造一个人为的概率过程，将它的某些参量视为问题的解。
从指定概率分布中采样。产生服从己知概率分布的随机变量是实现蒙特卡洛方法模拟试验的关键步骤。
建立各种估计量的估计。一般说来，构造出概率模型并能从中抽样后，便可进行现模拟试验。随后，就要确定一个随机变量，将其作为待求解问题的解进行估计。

在实际计算中， 通常无法直接从后验概率分布中采样，如何得到服从后验概率分布的随机样本是蒙特卡洛方法中基本的问题之一。重要性采样法引入一个已知的、容易采样的重要性概率密度函数 q ( x k ∣ Y k ) q(x_k|Y_k) q(xk∣Yk)，从中生成采样粒子，利用这些随机样本的加权和来逼近后验滤
波概率密度 p ( x k ∣ Y k ) p(x_k|Y_k) p(xk∣Yk) ，如图 2.3所示。

令{ x k ( i ) , w k ( i ) , i = 1 , . . . , N x_k^{(i)}, w_k^{(i)},i=1,...,N xk(i),wk(i),i=1,...,N表示一支撑点，其中 x k ( i ) x_k^{(i)} xk(i)是 k 时刻第 i 个粒子的状态，其相应的权值为$ w_k^{(i)}$ ，则后验滤波概率密度可以表示为

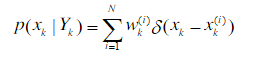
其中：

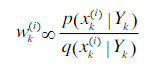
当采样粒子的数目很大时，便可近似逼近真实的后验概率密度函数。任意函数 f ( x k ) f(x_k) f(xk)的期望估计为

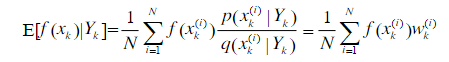
序贯重要性采样算法

在基于重要性采样的蒙特卡洛模拟方法中，估计后验滤波概率需要利用所有的观测数据，每次新的观测数据来到都需要重新计算整个状态序列的重要性权值。序贯重要性采样作为粒子滤波的基础，它将统计学中的序贯分析方法应用到的蒙特卡洛方法中，从而实现后验滤波概率密度的递推估计。假设重要性概率密度函数 q ( x 0 : k ∣ y 1 : k ) q(x_{0:k}|y_{1:k}) q(x0:k∣y1:k)可以分解为
q ( x 0 : k ∣ y 1 : k ) = q ( x 0 : k − 1 ∣ y 1 : k − 1 ) q ( x k ∣ x 0 : k − 1 ， y 1 : k − 1 ) q(x_{0:k}|y_{1:k})=q(x_{0:k-1}|y_{1:k-1}) q(x_k|x_{0:k-1}，y_{1:k-1}) q(x0:k∣y1:k)=q(x0:k−1∣y1:k−1)q(xk∣x0:k−1，y1:k−1)
设系统状态是一个马尔可夫过程，且给定系统状态下各次观测独立，则有

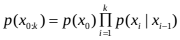
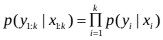
后验概率密度函数的递归形式可以表示为

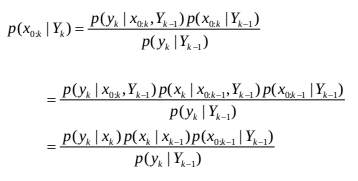
粒子权值 w k ( i ) w_k^{(i)} wk(i)的递归形式可以表示为

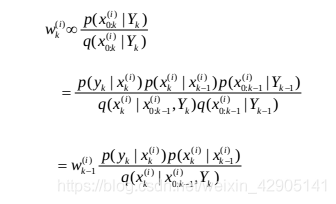
通常，需要对粒子权值进行归一化处理，即

序贯重要性采样算法从重要性概率密度函数中生成采样粒子，并随着测量值的依次到来递推求得相应的权值，最终以粒子加权和的形式来描述后验滤波概率密度，进而得到状态估计。序贯重要性采样算法的流程可以用如下伪代码描述：

重要密度函数的选择

重要性概率密度函数的选择对粒子滤波的性能有很大影响，在设计与实现粒子滤波器的过程中十分重要。在工程应用中，通常选取状态变量的转移概率密度函数作为重要性概率密度函数。此时，粒子的权值为

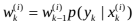
转移概率的形式简单且易于实现，在观测精度不高的场合，将其作为重要性概率密度函数可以取得较好的滤波效果。
然而，采用转移概率密度函数作为重要性概率密度函数没有考虑最新观测数据所提供的信息，从中抽取的样本与真实后验分布产生的样本存在一定的偏差，特别是当观测模型具有较高的精度或预测先验与似然函数之间重叠部分较少时，这种偏差尤为明显。
择重要性概率密度函数的一个标准是使得粒子权值的方差最小。Doucet等给出的最优重要性概率密度函数为

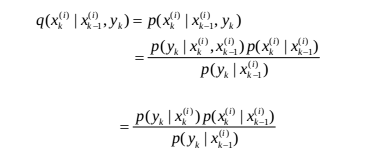
此时，粒子的权值为