1. 简介

无损卡尔曼滤波又称无迹卡尔曼滤波（Unscented Kalman Filter，UKF），是无损变换（Unscented Transform，UT）与标准卡尔曼滤波体系的结合，通过无损变换变换使非线性系统方程适用于线性假设下的标准卡尔曼体系。

UKF使用的是统计线性化技术，我们把这种线性化的方法叫做无损变换（unscented transformation）这一技术主要通过n个在先验分布中采集的点（我们把它们叫sigma points）的线性回归来线性化随机变量的非线性函数，由于我们考虑的是随机变量的扩展，所以这种线性化要比泰勒级数线性化（EKF所使用的策略）更准确。和EKF一样，UKF也主要分为预测和更新。

UKF的基本思想是卡尔曼滤波与无损变换，它能有效地克服EKF估计精度低、稳定性差的问题，因为不用忽略高阶项，所以对于非线性分布统计量的计算精度高。

2. CTRV运动模型

恒定转率和速度模型（Constant Turn Rate and Velocity，CTRV）

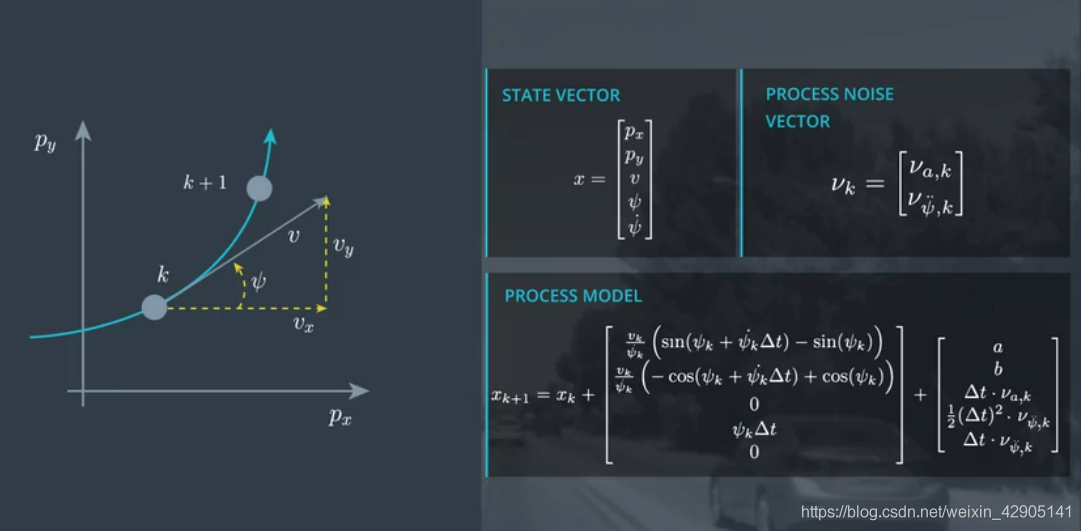
2.1 CTRV的目标状态量：

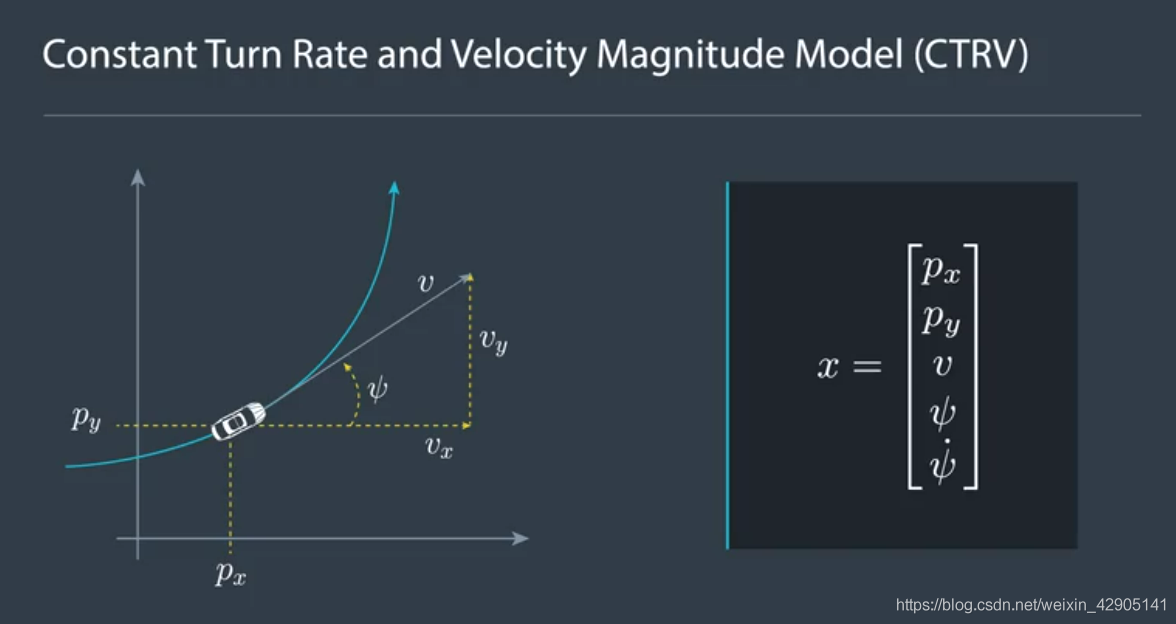
2.2 CTRV的状态转移函数：

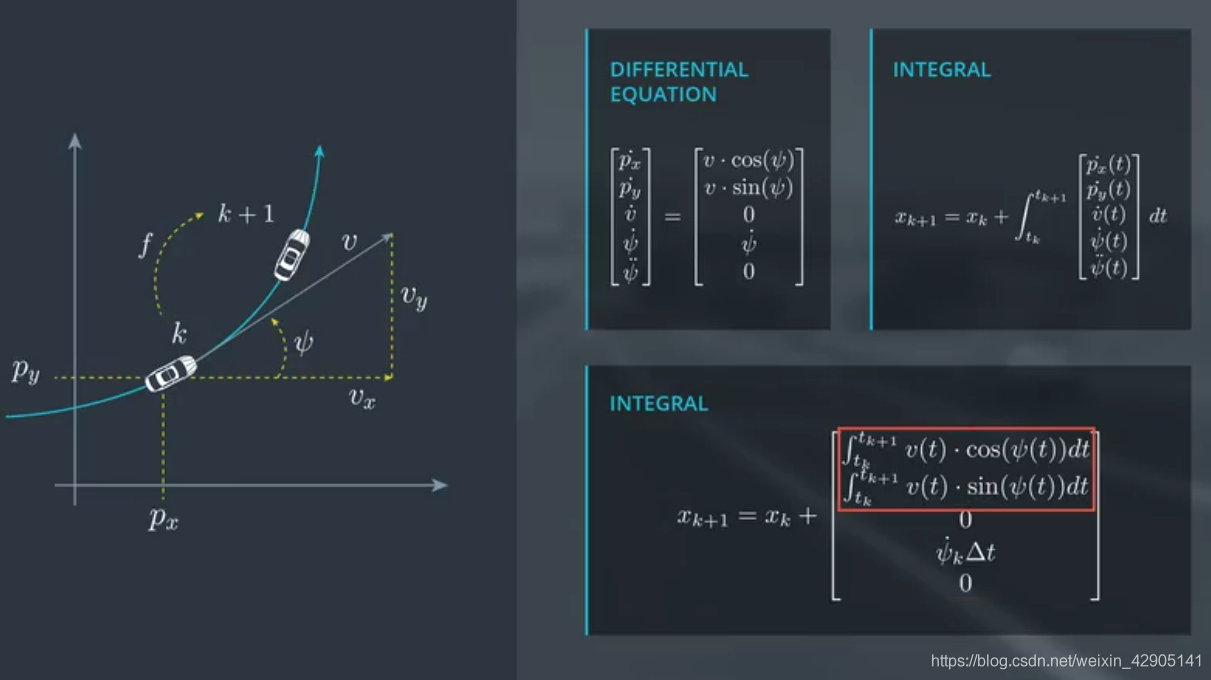
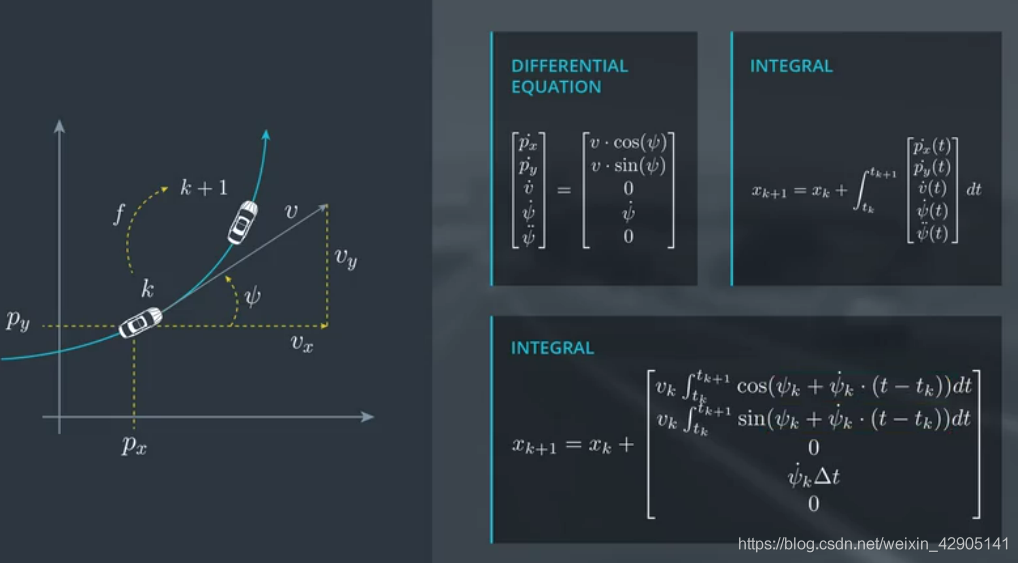
2.3 CTRV Process Noise

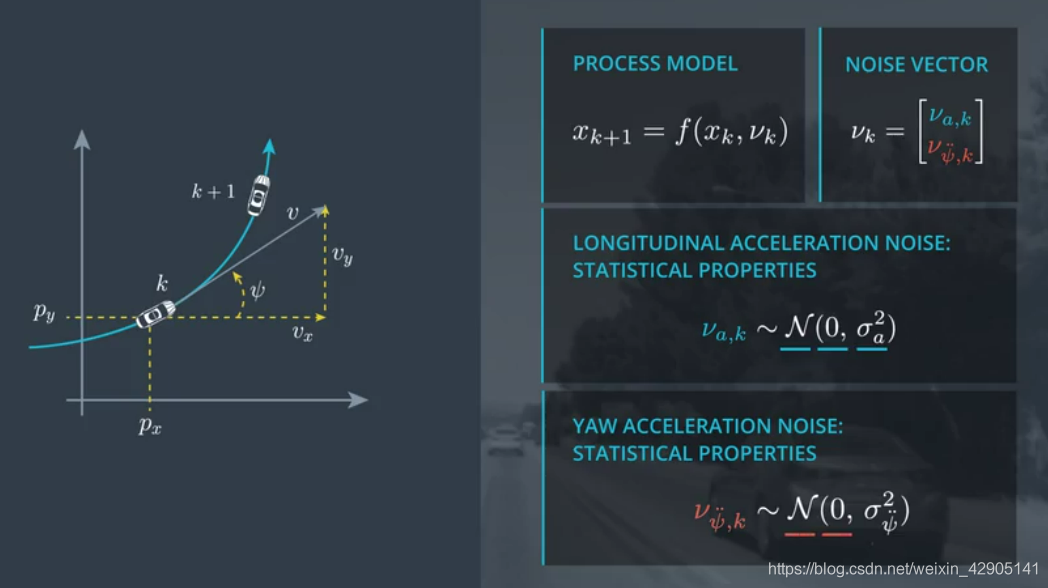
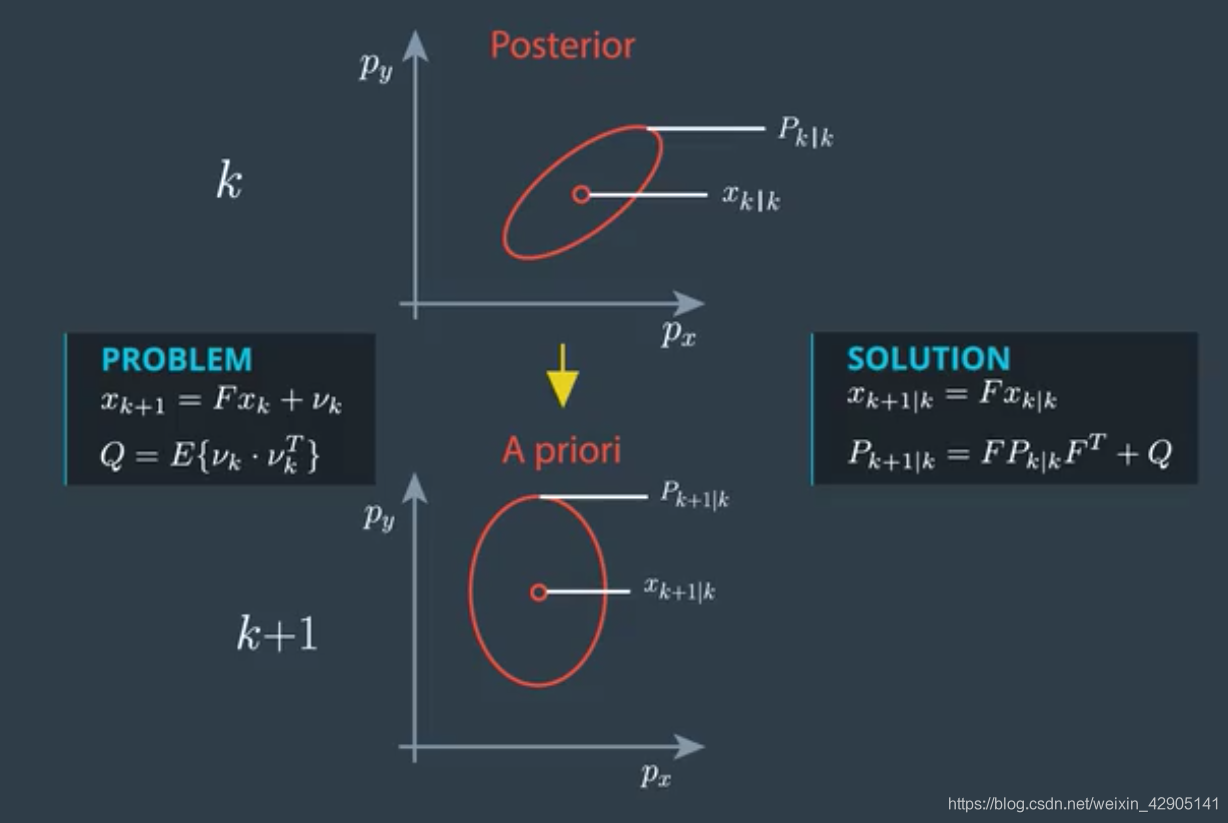
3. Prediction

分为3个步骤：

• 产生Sigma点
• 预测Sigma点的下一帧状态 （类似于粒子滤波中的预测，更新粒子状态）
• 预测系统状态的均值和方差（类似于粒子滤波中的加权平均）

3.1 Generate Sigma Points

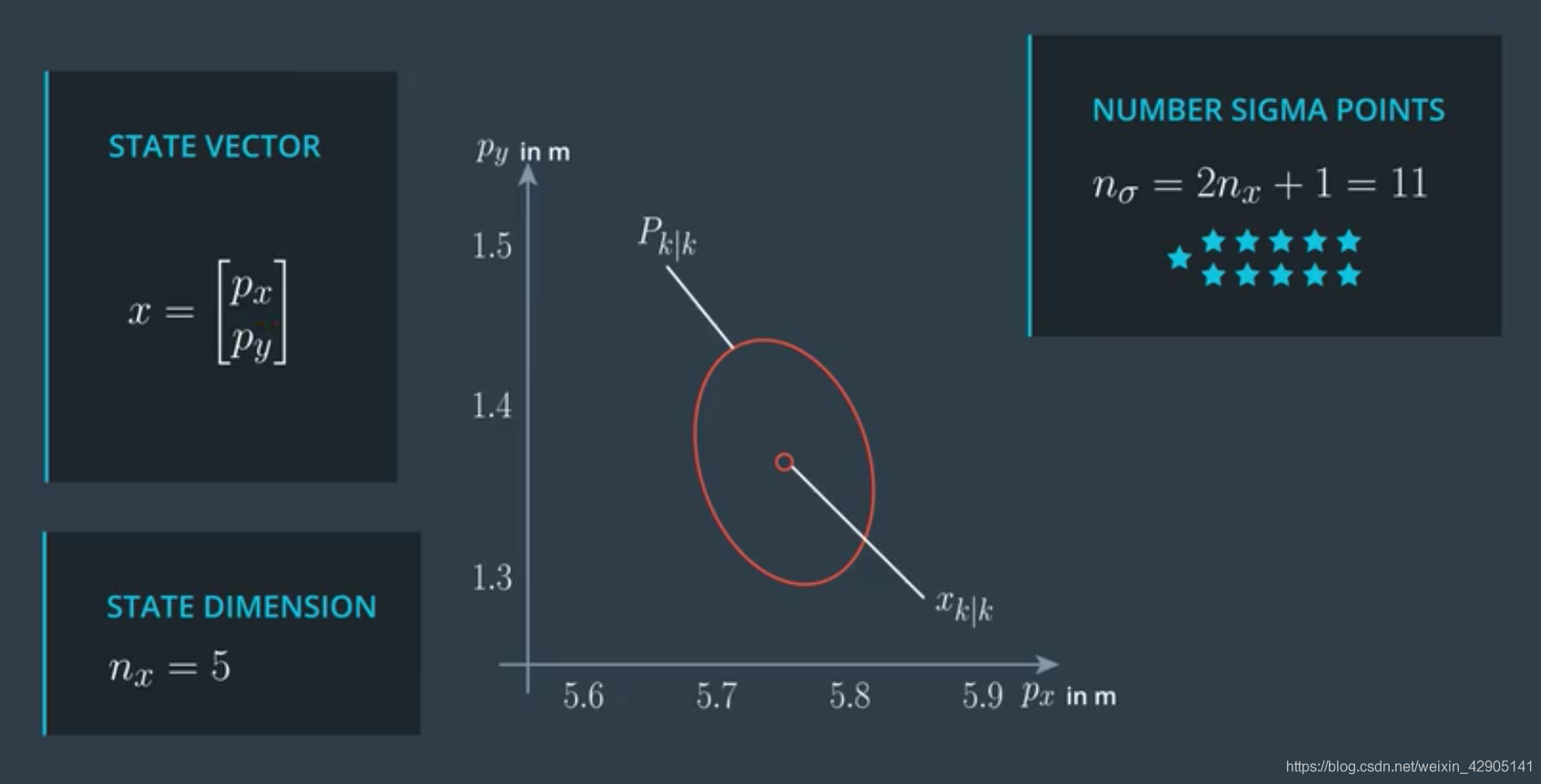
通常，假定状态的个数为 n ，我们会产生 2n+1 个sigma点，其中第一个就是我们当前状态的均值 μ ，sigma点集的均值的计算公式为：
χ [ 1 ] = μ \chi^{[ 1 ]} = \mu χ[1]=μ
χ [ i ] = μ + ( ( n + λ ) P ) i f o r    i = 2 , . . . , n + 1 \chi^{[i]} = \mu + \left( \sqrt {(n + \lambda)P}\right)_i \quad for \ \ i=2, ..., n+1 χ[i]=μ+((n+λ)P ​)i​for  i=2,...,n+1
χ [ i ] = μ − ( ( n + λ ) P ) i − n f o r    i = n + 2 , . . . , 2 n + 1 \chi^{[i]} = \mu - \left( \sqrt {(n + \lambda)P} \right)_{i-n} \quad for \ \ i=n+2, ..., 2n+1 χ[i]=μ−((n+λ)P ​)i−n​for  i=n+2,...,2n+1
其中的 λ 是一个超参数，根据公式，λ 越大， sigma点就越远离状态的均值，λ 越小， sigma点就越靠近状态的均值。

在我们的CTRV模型中，状态数量 n 除了要包含5个状态以外，还要包含处理噪声 μa 和 μω˙,因为这些处理噪声对模型也有着非线性的影响。在增加了处理噪声的影响以后，我们的不确定性矩阵 P 就变成了：
P = ( P ′ 0 0 Q ) P = \left( \begin{array}{c} P' & 0 \\ 0 & Q \end{array} \right) P=(P′0​0Q​)
其中，P′ 就是我们原来的不确定性矩阵（在CTRV模型中就是一个 5×5 的矩阵），Q是处理噪声的协方差矩阵，在CTRV模型中考虑到直线加速度核Q的形式为：

计算增广的Sigma Points

3.2 预测sigma point

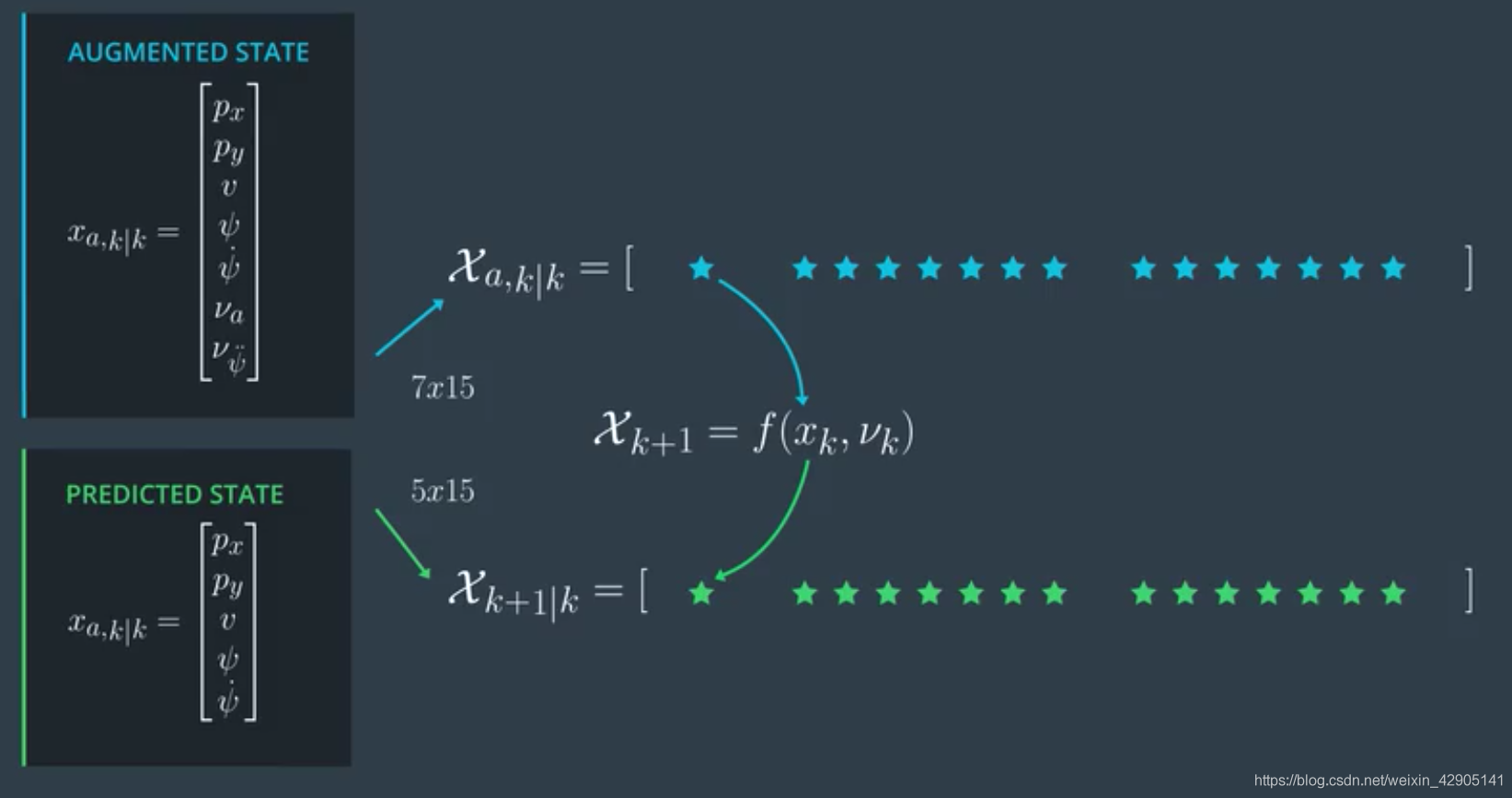
现在我们有sigma点集，根据process model g ( χ k , μ k ) g(\chi_k, \mu_k) g(χk​,μk​)预测未来的Sigma点 X k + 1 ∣ k X_{k+1|k} Xk+1∣k​

χ k + 1 = g ( χ k , μ k ) \chi_{k+1} = g(\chi_k, \mu_k) χk+1​=g(χk​,μk​)
需要注意的是，这里的输入 χ k \chi_k χk​ 是一个 (7,15)的矩阵（因为考虑了两个噪声量），但是输出 χ k + 1 ∣ k \chi_{k+1 | k} χk+1∣k​是一个(5,15)的矩阵（因为这是预测的结果，本质上是基于运动模型的先验，先验中的均值不应当包含 a , ω ˙ a , ω˙ a,ω˙这类不确定的量）

3.3 预测均值和方差

根据预测的Sigma点 X k + 1 ∣ k X_{k+1|k} Xk+1∣k​生成状态预测 x k + 1 ∣ k , P k + 1 ∣ k x_{k+1|k}, P_{k+1|k} xk+1∣k​,Pk+1∣k​

1. 首先要计算出各个sigma点的权重，权重的计算公式为：
   w i = λ λ + n σ , i = 1 w_{i} = \frac{\lambda}{\lambda + n_{\sigma}}, \quad i = 1 wi​=λ+nσ​λ​,i=1.
   w i = 1 2 ( λ + n σ ) , i = 2 , . . . , 2 n σ + 1 w_{i} = \frac{1}{2(\lambda + n_{\sigma})}, \quad i = 2, ..., 2n_{\sigma}+1 wi​=2(λ+nσ​)1​,i=2,...,2nσ​+1

2. 然后基于每个sigma点的权重去求新的分布的均值和方差：
   
   x k + 1 ∣ k x_{k+1|k} xk+1∣k​是sigma点集中每个点各个状态量的加权和， P′ 即为先验分布的协方差（不确定性） P k + 1 ∣ k P_{k+1|k} Pk+1∣k​ ， 由每个sigma点的方差的加权和求得。

4. Update

4.1 Predict Measurement

将先验映射到测量空间然后算出均值和方差:
测量分为两个部分，LIDAR测量和RADAR测量，其中LIDAR测量模型本身就是线性的，所以我们重点还是放在RADAR测量模型的处理上面，RADAR的测量f非线性映射函数为：
h ( x ) = [ ρ ϕ ρ ˙ ] = [ p x 2 + p y 2 arctan ⁡ p y p x p x v x + p y v y p x 2 + p y 2 ] h(x) = \left[ \begin{matrix} \rho \\ \phi \\ \dot{\rho} \end{matrix} \right] = \left[ \begin{matrix} \sqrt{p_x^2+p_y^2} \\ \arctan{\frac{p_y}{p_x}} \\ \frac{p_x v_x + p_y v_y}{\sqrt{p_x^2+p_y^2} } \end{matrix}\right] h(x)=⎣⎡​ρϕρ˙​​⎦⎤​=⎣⎢⎢⎡​px2​+py2​ ​arctanpx​py​​px2​+py2​ ​px​vx​+py​vy​​​⎦⎥⎥⎤​
Measurement model如图所示：

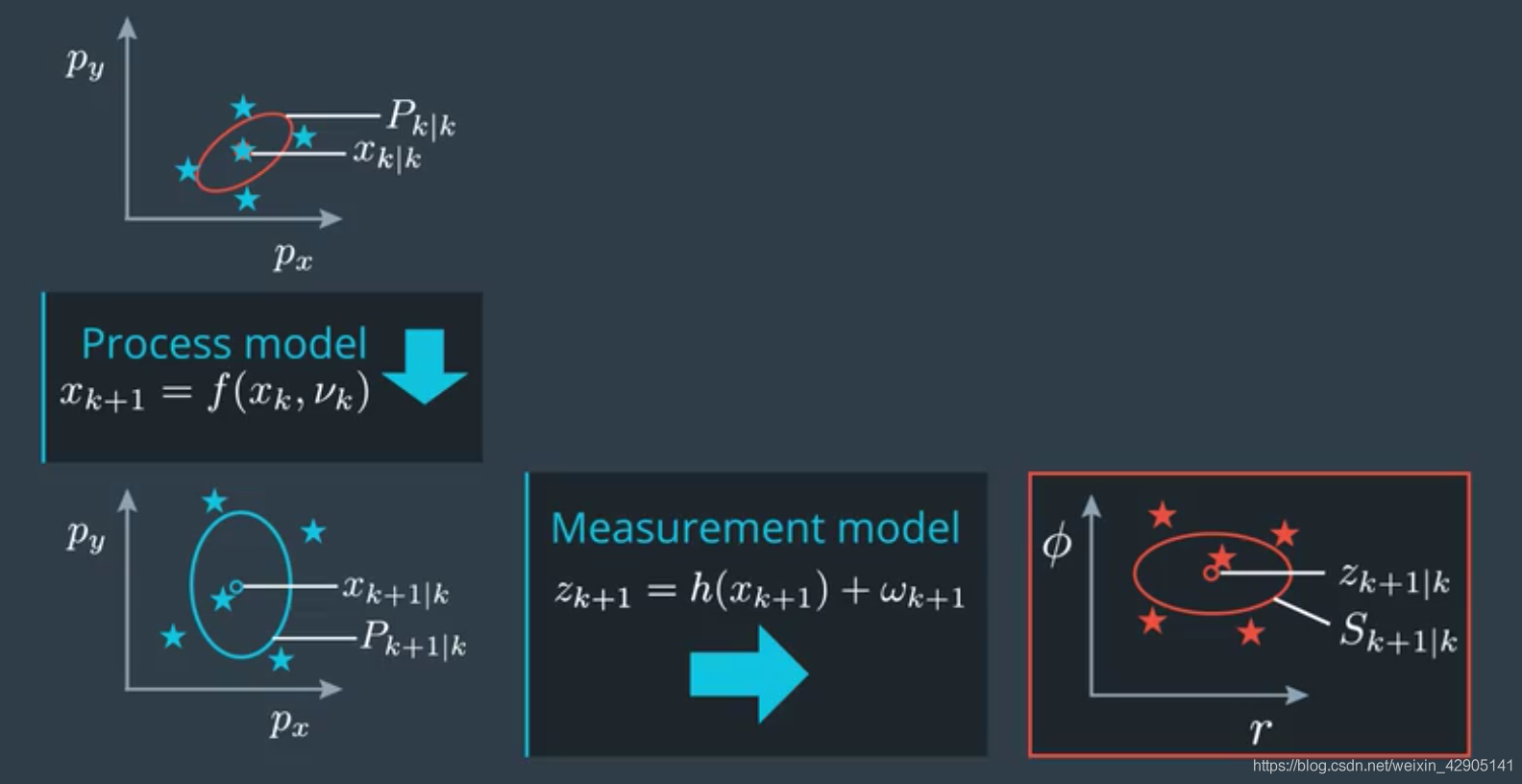
再一次，我们使用无损转换来解决，但是这里，我们可以不用再产生sigma points了，我们可以直接使用预测出来的sigma点集，并且可以忽略掉处理噪声部分。那么对先验的非线性映射就可以表示为如下的sigma point预测（即预测非线性变换以后的均值和协方差）：


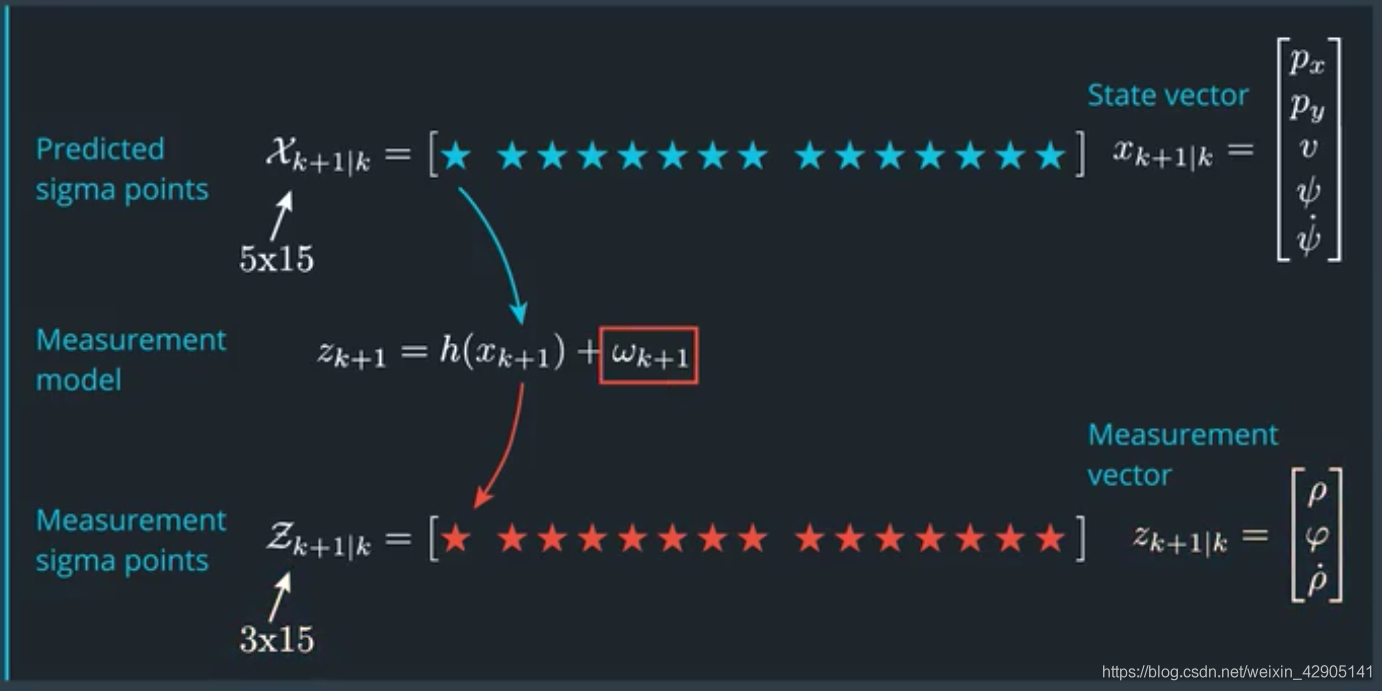
这里的 R 也是测量噪声，在这里我们直接将测量噪声的协方差加到测量协方差上是因为该噪声对系统没有非线性影响。在本例中，以RADAR的测量为例，那么测量噪声R为：
R = E [ w w T ] = ( σ ρ 2 0 0 0 σ ψ 2 0 0 0 σ ρ ˙ 2 ) R = E[ww^T] = \left(\begin{matrix} \sigma_{\rho}^2 & 0 & 0 \\ 0 & \sigma_{\psi}^2 & 0 \\ 0 & 0 & \sigma_{\dot\rho}^2 \\ \end{matrix}\right) R=E[wwT]=⎝⎛​σρ2​00​0σψ2​0​00σρ˙​2​​⎠⎞​

4.2 Update State

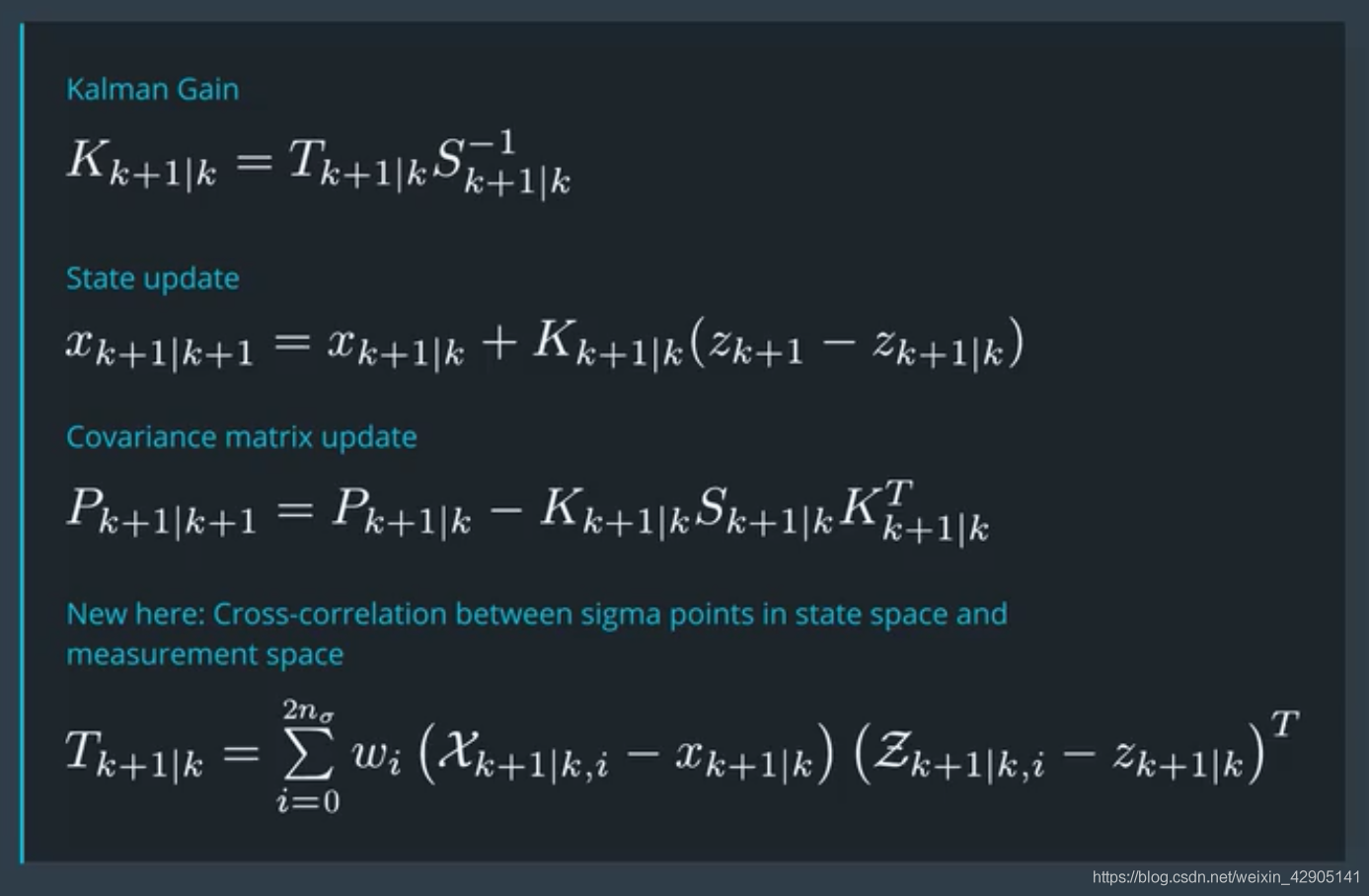
• 首先计算出sigma点集在状态空间和测量空间的互相关函数 T k + 1 ∣ k T_{k+1|k} Tk+1∣k​
• 计算卡尔曼增益 K k + 1 ∣ k K_{k+1|k} Kk+1∣k​
• 更新状态，计算$x_{k+1|k+1}（其中 z k + 1 z_{k+1} zk+1​ 是新得到的测量，而 z k + 1 ∣ k z_{k+1|k} zk+1∣k​ 则是我们根据先验计算出来的在测量空间的测量)。
• 更新状态协方差矩阵，计算 P k + 1 ∣ k + 1 P_{k+1|k+1} Pk+1∣k+1​