拓扑排序

一个无环的有向图称为无环图（Directed Acyclic Graph），简称DAG图。

在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系，这样的有向图为顶点表示活动的网，我们称之为AOV网（Active On Vertex Network）。

拓扑序列：设G=(V,E)是一个具有n个顶点的有向图，V中的顶点序列V1,V2,……,Vn满足若从顶点Vi到Vj有一条路径，则在顶点序列中顶点Vi必在顶点Vj之前。则我们称这样的顶点序列为一个拓扑序列。

现在举个例子，如下图所示:

其中拓扑图如下：

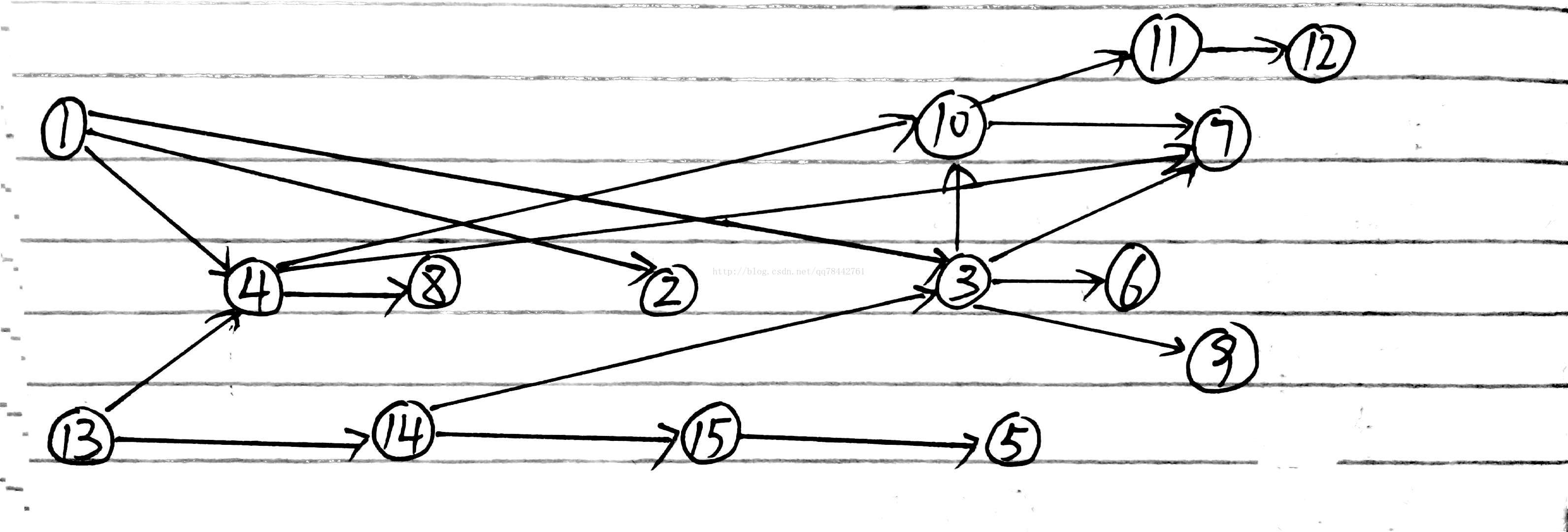
可以做邻接矩阵

下面是代码：

// 边表结点声明
typedef struct EdgeNode
{
	int adjvex;
	struct EdgeNode *next;
}EdgeNode;

// 顶点表结点声明
typedef struct VertexNode
{
	int in;			// 顶点入度
	int data;
	EdgeNode *firstedge;
}VertexNode, AdjList[MAXVEX];

typedef struct
{
	AdjList adjList;
	int numvertexes, numEdges;
}graphAdjList, *GraphAdjList;

// 拓扑排序算法
// 若GL无回路，则输出拓扑排序序列并返回OK，否则返回ERROR
Status TopologicalSort(GraphAdjList GL)
{
	EdgeNode *e;
	int i, k, gettop;
	int top = 0;		// 用于栈指针下标索引
	int count = 0;		// 用于统计输出顶点的个数
	int *stack;			// 用于存储入度为0的顶点
	
	stack = (int *)malloc(GL->numVertexes * sizeof(int));
	
	for( i=0; i < GL->numVertexes; i++ )
	{
		if( 0 == GL->adjList[i].in )
		{
			stack[++top] = i;	// 将度为0的顶点下标入栈
		}
	}
	
	while( 0 != top )
	{
		gettop = stack[top--];	// 出栈
		printf("%d -> ", GL->adjList[gettop].data);
		count++;				
		
		for( e=GL->adjList[gettop].firstedge; e; e=e->next )
		{
			k = e->adjvex;
			// 注意：下边这个if条件是分析整个程序的要点！
			// 将k号顶点邻接点的入度-1，因为他的前驱已经消除
			// 接着判断-1后入度是否为0，如果为0则也入栈
			if( !(--GL->adjList[k].in) )	
			{
				stack[++top] = k;
			}
		}
	}
	
	if( count < GL->numVertexes )	// 如果count小于顶点数，说明存在环
	{
		return ERROR;
	}
	else
	{
		return OK;
	}
}