二叉查找树
二叉查找树,也称二叉搜索树,或二叉排序树。其定义也比较简单,要么是一颗空树,要么就是具有如下性质的二叉树:
(1)若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2) 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(3) 任意节点的左、右子树也分别为二叉查找树;
(4) 没有键值相等的节点。
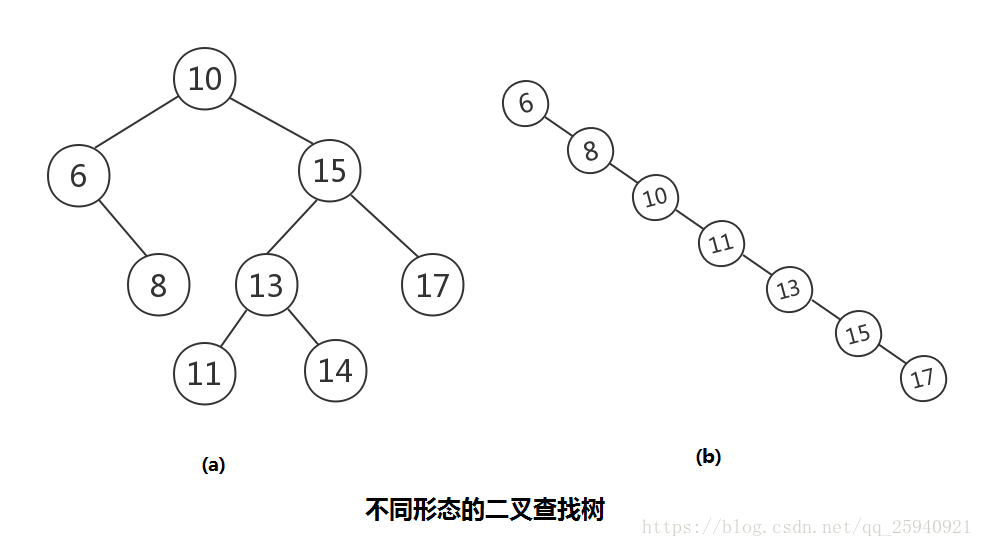
如上图所示,是不同形态的二叉查找树。二叉查找树是对要查找的数据进行生成树,左支的值小于右支的值。在查找的时候也是一样的思路,从根节点开始,比节点大进入右支,比节点小进入左支,直到查找到目标值。
二叉查找树的插入算法比较简单:空树,就首先生成根节点;不是空树就按照查找的算法,找到父节点,然后作为叶子节点插入,如果值已经存在就插入失败。
删除操作稍微复杂一点,有如下几种情况:
(1)如果删除的是叶节点,可以直接删除;
(2)如果被删除的元素有一个子节点,可以将子节点直接移到被删除元素的位置;
(3)如果有两个子节点,这时候就采用中序遍历,找到待删除的节点的后继节点,将其与待删除的节点互换,此时待删除节点的位置已经是叶子节点,可以直接删除。如下图:
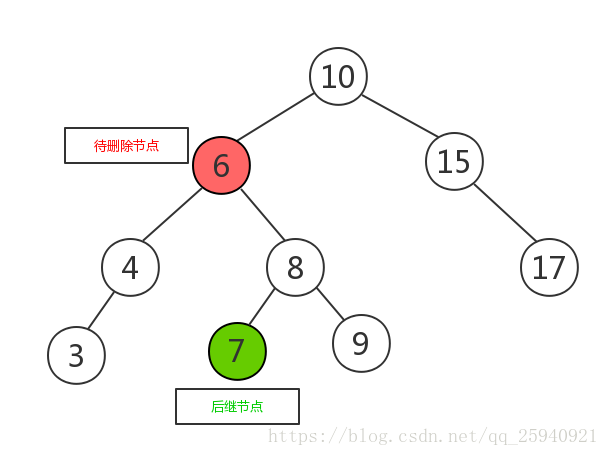
将待删除节点与后继节点互换,变成如下图所示:
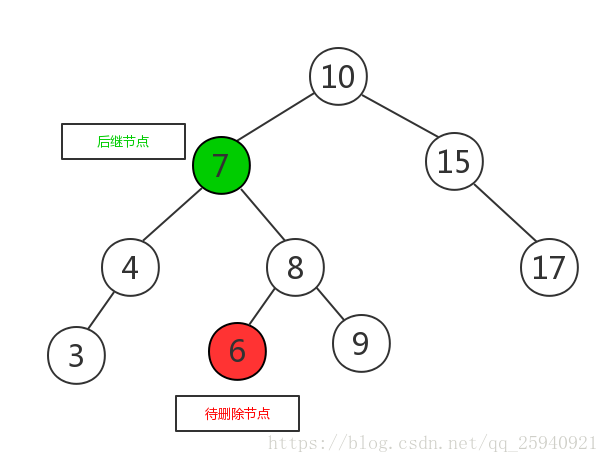
将待删除元素删除,如下图所示:
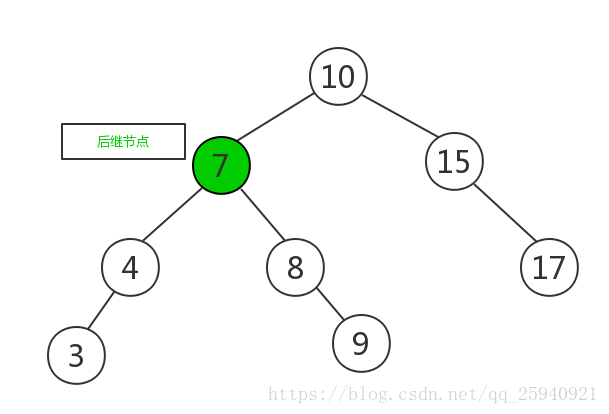
另外,二叉查找树还有一个性质,即对二叉查找树进行中序遍历,即可得到有序的数列。
二叉查找树的查询复杂度,和二分查找一样,插入和查找的时间复杂度均为 O(logn) ,但是在最坏的情况下仍然会有 O(n) 的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡(如上不同形态的二叉树图中的b)。
平衡二叉树
平衡二叉搜索树,又被称为AVL树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。 —-来自百度百科
由于普通的二叉查找树会容易失去”平衡“,极端情况下,二叉查找树会退化成线性的链表,导致插入和查找的复杂度下降到 O(n) ,所以,这也是平衡二叉树设计的初衷。那么平衡二叉树如何保持”平衡“呢?根据定义,有两个重点,一是左右两子树的高度差的绝对值不能超过1,二是左右两子树也是一颗平衡二叉树。
如下图所示,左图是一棵平衡二叉树,根节点10,左右两子树的高度差是1,而右图,虽然根节点左右两子树高度差是0,但是右子树15的左右子树高度差为2,不符合定义,所以右图不是一棵平衡二叉树。

由此可以看出平衡二叉树是一棵高度平衡的二叉查找树。所以,要构建跟维系一棵平衡二叉树就比普通的二叉树要复杂的多。在构建一棵平衡二叉树的过程中,当有新的节点要插入时,检查是否因插入后而破坏了树的平衡,如果是,则需要做旋转去改变树的结构。
关于旋转,这东西不拿动态图将还真很难讲明白。所以我就借一下 最容易懂得红黑树 这篇文章中左旋右旋的图来讲。
左旋:
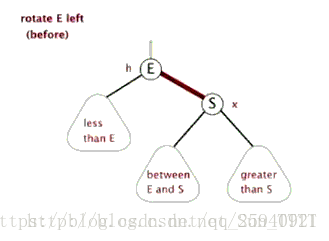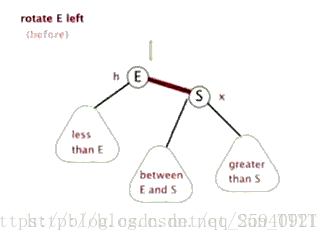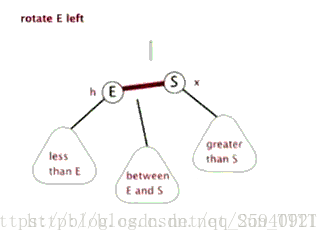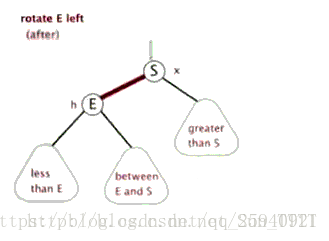
右旋:

不同于顺时针跟逆时针变换这种方式去记忆,上面两个动态图特别方便记忆跟理解:
左旋就是将节点的右支往左拉,右子节点变成父节点,并把晋升之后多余的左子节点出让给降级节点的右子节点;
而右旋就是反过来,将节点的左支往右拉,左子节点变成了父节点,并把晋升之后多余的右子节点出让给降级节点的左子节点。
即左旋就是往左变换,右旋就是往右变换。不管是左旋还是右旋,旋转的目的都是将节点多的一支出让节点给另一个节点少的一支。
举个例子,像上图是否平衡二叉树的图里面,左图在没插入前”19“节点前,该树还是平衡二叉树,但是在插入”19“后,导致了”15“的左右子树失去了”平衡“,所以此时可以将”15“节点进行左旋,让”15“自身把节点出让给”17“作为”17“的左树,使得”17“节点左右子树平衡,而”15“节点没有子树,左右也平衡了。如下图,

由于在构建平衡二叉树的时候,当有新节点插入时,都会判断插入后时候平衡,这说明了插入新节点前,都是平衡的,也即高度差绝对值不会超过1。当新节点插入后,有可能会有导致树不平衡,这时候就需要进行调整,而可能出现的情况就有4种,分别称作左左,左右,右左,右右。
左左:
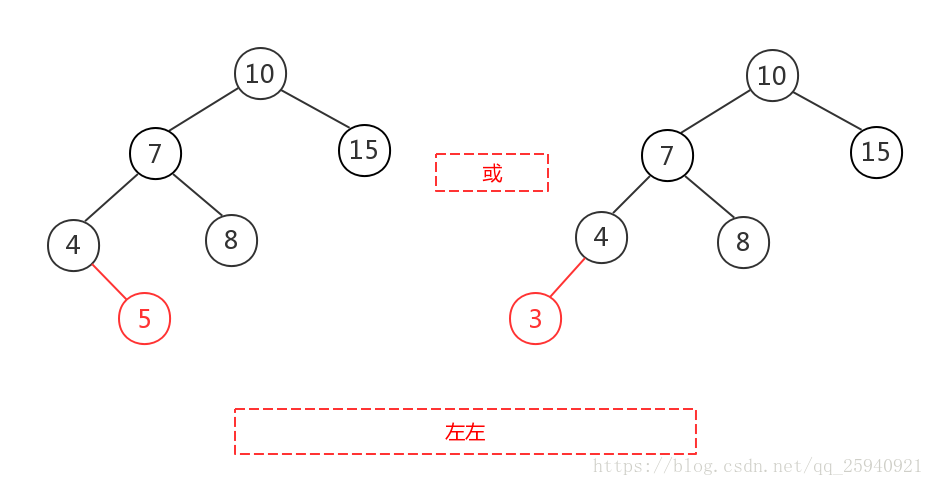
左左即为在原来平衡的二叉树上,在节点的左子树的左子树下,有新节点插入,导致节点的左右子树的高度差为2,如上即为”10“节点的左子树”7“,的左子树”4“,插入了节点”5“或”3“导致失衡。
左左调整其实比较简单,只需要对节点进行右旋即可,如下图,对节点”10“进行右旋,
注意:如果对左右旋变换还不是很懂或不是很熟练的,可以对照着前面的那两个动图去想象,自己动手变换几次,就明白了。
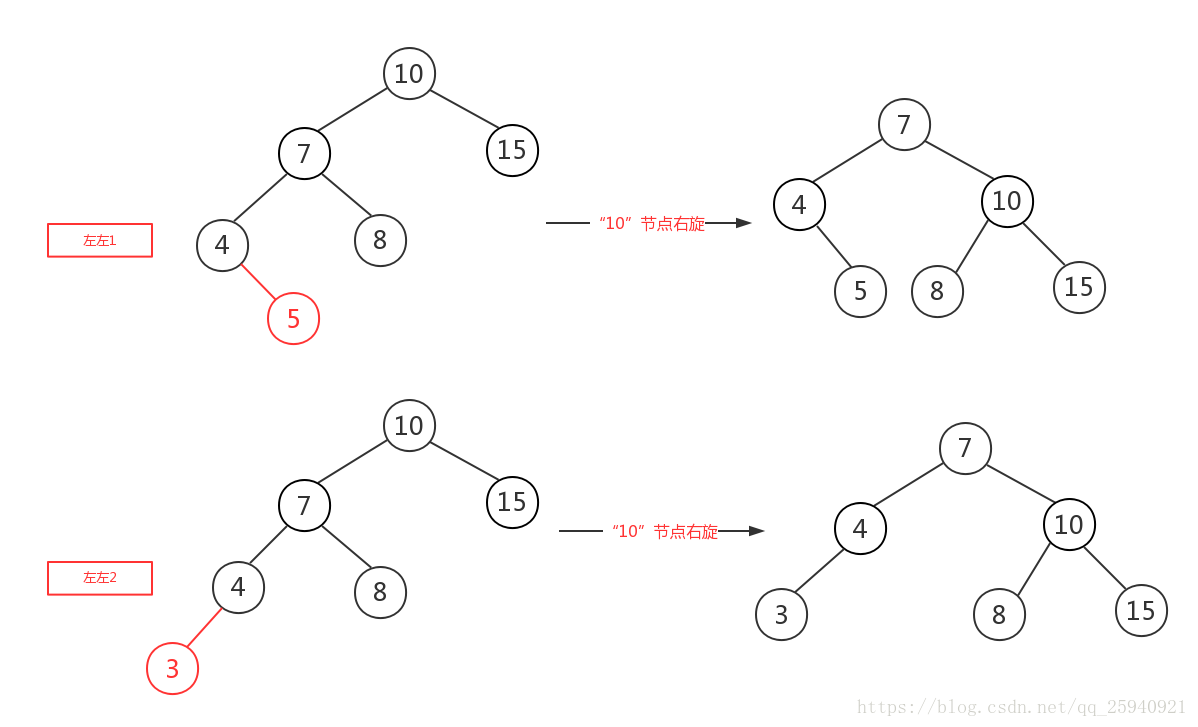
左右:
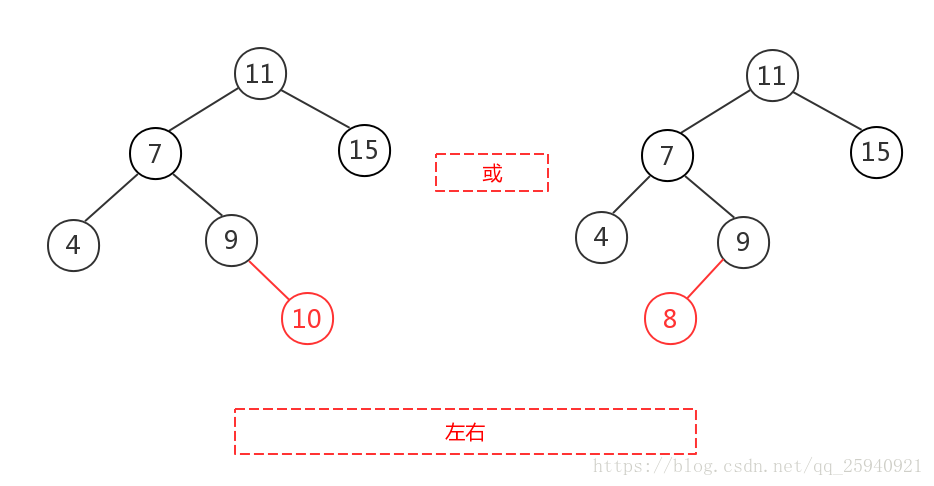
左右即为在原来平衡的二叉树上,在节点的左子树的右子树下,有新节点插入,导致节点的左右子树的高度差为2,如上即为”11“节点的左子树”7“,的右子树”9“,插入了节点”10“或”8“导致失衡。
左右的调整就不能像左左一样,进行一次旋转就完成调整。我们不妨先试着让左右像左左一样对”11“节点进行右旋,结果图如下,右图的二叉树依然不平衡,而右图就是接下来要讲的右左,即左右跟右左互为镜像,左左跟右右也互为镜像。

右右跟左左一样,只需要旋转一次就能把树调整平衡,而左右跟右左也一样,都要进行旋转两次才能把树调整平衡,所以,首先上图的这种调整是错误的,正确的调整方式是,将左右进行第一次旋转,将左右先调整成左左,然后再对左左进行调整,从而使得二叉树平衡。
即先对上图的节点”7“进行左旋,使得二叉树变成了左左,之后再对”11“节点进行右旋,此时二叉树就调整完成,如下图,
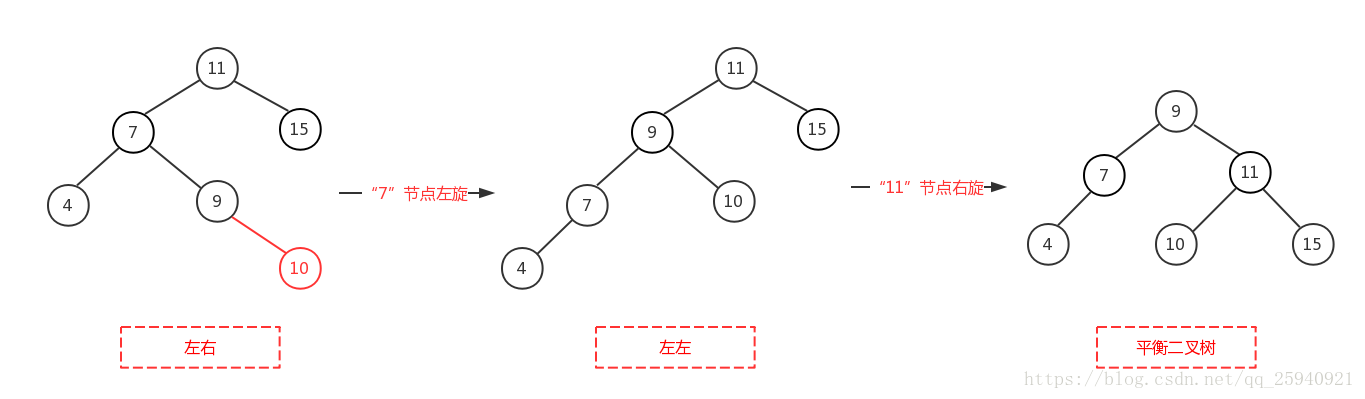
右左:

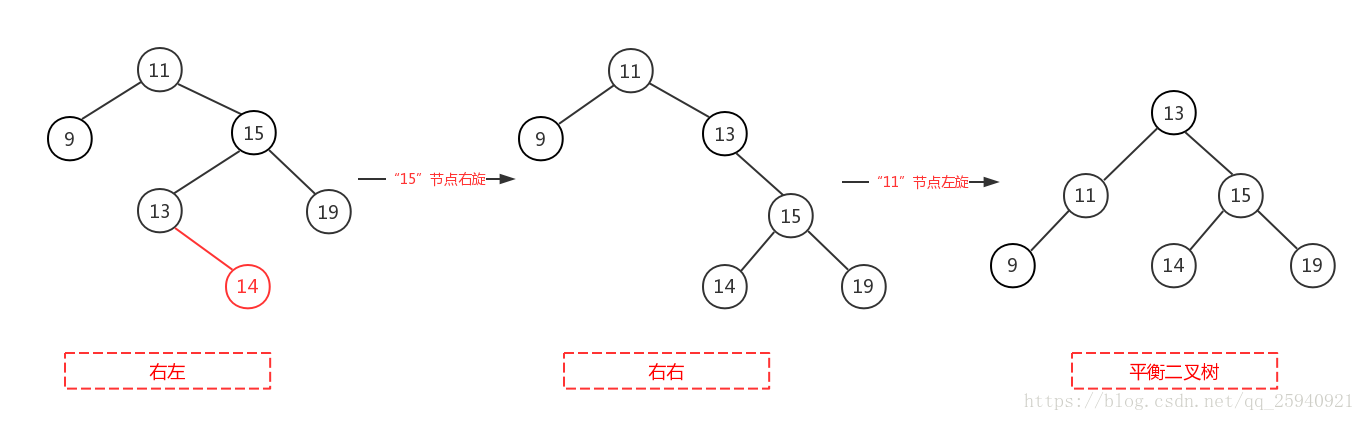
右左即为在原来平衡的二叉树上,在节点的右子树的左子树下,有新节点插入,导致节点的左右子树的高度差为2,如上即为”11“节点的右子树”15“,的左子树”13“,插入了节点”12“或”14“导致失衡。
前面也说了,右左跟左右其实互为镜像,所以调整过程就反过来,先对节点”15“进行右旋,使得二叉树变成右右,之后再对”11“节点进行左旋,此时二叉树就调整完成,如下图,
右右:
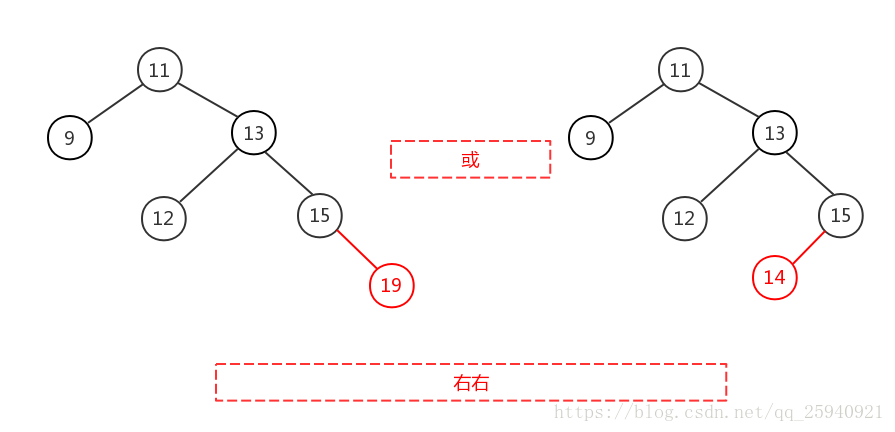
右右即为在原来平衡的二叉树上,在节点的右子树的右子树下,有新节点插入,导致节点的左右子树的高度差为2,如上即为”11“节点的右子树”13“,的左子树”15“,插入了节点”14“或”19“导致失衡。
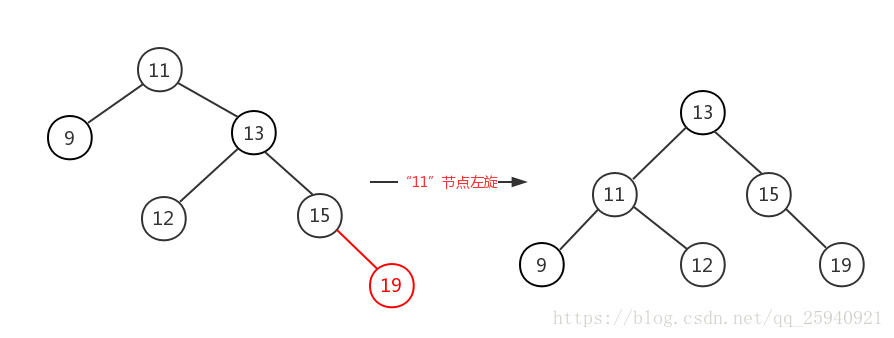
右右只需对节点进行一次左旋即可调整平衡,如下图,对”11“节点进行左旋。
平衡二叉树构建的过程,就是节点插入的过程,插入失衡情况就上面4种,算简单了,下面讲下平衡二叉树节点的删除,删除的情况会复杂一点,复杂的原因主要在于删除了节点之后要维系二叉树的平衡,但是删除二叉树节点总结起来就两个判断:①删除的是什么类型的节点?②删除了节点之后是否导致失衡?
节点的类型有三种:1.叶子节点;2.只有左子树或只有右子树;3.既有左子树又有右子树。
针对这三种节点类型,再引入判断②,所以处理思路分别是:
(1)当删除的节点是叶子节点,则将节点删除,然后从父节点开始,判断是否失衡,如果没有失衡,则再判断父节点的父节点是否失衡,直到根节点,此时到根节点还发现没有失衡,则说此时树是平衡的;如果中间过程发现失衡,则判断属于哪种类型的失衡(左左,左右,右左,右右),然后进行调整。
(2)删除的节点只有左子树或只有右子树,这种情况其实就比删除叶子节点的步骤多一步,就是将节点删除,然后把仅有一支的左子树或右子树替代原有结点的位置,后面的步骤就一样了,从父节点开始,判断是否失衡,如果没有失衡,则再判断父节点的父节点是否失衡,直到根节点,如果中间过程发现失衡,则根据失衡的类型进行调整。
(3)删除的节点既有左子树又有右子树,这种情况又比上面这种多一步,就是中序遍历,找到待删除节点的前驱或者后驱都行,然后与待删除节点互换位置,然后把待删除的节点删掉,后面的步骤也是一样,判断是否失衡,然后根据失衡类型进行调整。
最后总结一下,平衡二叉树是一棵高度平衡的二叉树,所以查询的时间复杂度是 O(logN) 。插入的话上面也说,失衡的情况有4种,左左,左右,右左,右右,即一旦插入新节点导致失衡需要调整,最多也只要旋转2次,所以,插入复杂度是 O(1) ,但是平衡二叉树也不是完美的,也有缺点,从上面删除处理思路中也可以看到,就是删除节点时有可能因为失衡,导致需要从删除节点的父节点开始,不断的回溯到根节点,如果这棵平衡二叉树很高的话,那中间就要判断很多个节点。所以后来也出现了综合性能比其更好的树—-红黑树,后面再讲。

 菜鸟笔记
菜鸟笔记