一、概念
二叉树遍历分为三种:前序、中序、后序,其中序遍历最为重要。
二、特点

A:根节点、B:左节点、C:右节点;
- 前序顺序是ABC(根节点排最先,然后同级先左后右);
- 中序顺序是BAC (先左后根最后右);
- 后序顺序是BCA(先左后右最后根)。
三、图
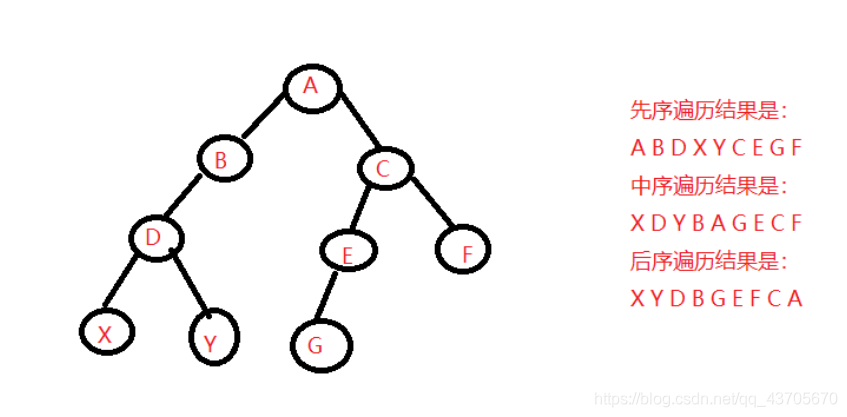
四、代码实现
递归方式
第一步: 节点实体类
package node.tree;
public class Node {
private String value;
private Node left;
private Node right;
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
public Node(String value, Node left, Node right) {
this.value = value;
this.left = left;
this.right = right;
}
@Override
public String toString() {
return "Node{" +
"value='" + value + '\'' +
", left=" + left +
", right=" + right +
'}';
}
}
二:节点数和核心处理类
package node.tree;
import java.util.ArrayList;
import java.util.List;
public class Tree {
private Node root;
private List<Node> result=new ArrayList<Node>();
public Node getRoot() {
return root;
}
public void setRoot(Node root) {
this.root = root;
}
public List<Node> getResult() {
return result;
}
public void setResult(List<Node> result) {
this.result = result;
}
public Tree(){
init();
}
private void init() {
Node g=new Node("G",null,null);
Node x=new Node("X",null,null);
Node y=new Node("Y",null,null);
Node d=new Node("D",x,y);
Node b=new Node("B",d,null);
Node e=new Node("E",g,null);
Node f=new Node("F",null,null);
Node c=new Node("C",e,f);
Node a=new Node("A",b,c);
root=a;
}
/**
* 计算深度
* @param node
* @return
*/
public int calDepth(Node node){
if (node.getLeft()==null&&node.getRight()==null){
return 1;
}
int leftDepth=0;
int rightDepth=0;
if(node.getLeft()!=null){
leftDepth=calDepth(node.getLeft());
}
if(node.getRight()!=null){
rightDepth=calDepth(node.getRight());
}
System.out.println("左"+leftDepth+"右"+rightDepth);
int temp=leftDepth>rightDepth?leftDepth+1:rightDepth+1;
System.out.println("中间计算结果"+temp);
return temp;
}
//前序遍历 根左右
public void perOrder(Node root){
if(root==null){
return;
}
result.add(root);
if(root.getLeft()!=null){
perOrder(root.getLeft());
}
if(root.getRight()!=null){
perOrder(root.getRight());
}
}
//中序遍历 左根右
public void InMiddleOrder(Node root){
if(root==null){
return;
}
if(root.getLeft()!=null){
InMiddleOrder(root.getLeft());
}
result.add(root);
if(root.getRight()!=null){
InMiddleOrder(root.getRight());
}
}
//后序遍历 左右根
public void LastOrder(Node root){
if(root==null){
return;
}
if(root.getLeft()!=null){
LastOrder(root.getLeft());
}
if(root.getRight()!=null){
LastOrder(root.getRight());
}
result.add(root);
}
}
三:测试类
package node.tree;
public class Test {
public static void main(String[] args) {
Tree tree=new Tree();
System.out.println("根节点"+tree.getRoot().getValue());
//先序遍历
tree.perOrder(tree.getRoot());
System.out.println("树的深度是"+tree.calDepth(tree.getRoot()));
System.out.println("先序遍历结果是:");
for (Node node :tree.getResult() ) {
System.out.print(node.getValue()+" ");
}
System.out.println("");
tree.getResult().clear();
tree.InMiddleOrder(tree.getRoot());
System.out.println("中序遍历结果是:");
for (Node node :tree.getResult() ) {
System.out.print(node.getValue()+" ");
}
System.out.println("");
tree.getResult().clear();
tree.LastOrder(tree.getRoot());
System.out.println("后序遍历结果是:");
for (Node node :tree.getResult() ) {
System.out.print(node.getValue()+" ");
}
}
}
非递归方式实现
前序遍历:
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int v) {
value = v;
}
}
// Object peek( )
// 查看堆栈顶部的对象,但不从堆栈中移除它。
// Object pop( )
// 移除堆栈顶部的对象,并作为此函数的值返回该对象。
// Object push(Object element)
// 把项压入堆栈顶部。
// 先头节点,先压右,后压左
public static void pre(Node head) {
// 压栈
System.out.print("pre-order: ");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
stack.add(head);
while (!stack.isEmpty()) {
// 弹出来
head = stack.pop();
System.out.print(head.value + " ");
if (head.right != null) {
// 压右
stack.push(head.right);
}
if (head.left != null) {
// 压右
stack.push(head.left);
}
}
}
System.out.println();
}
后序遍历方式:
public static void pos1(Node head) {
System.out.print("pos-order: ");
if (head != null) {
Stack<Node> s1 = new Stack<Node>();
Stack<Node> s2 = new Stack<Node>();
s1.push(head);
while (!s1.isEmpty()) {
head = s1.pop(); // 头 右 左
s2.push(head);
if (head.left != null) {
s1.push(head.left);
}
if (head.right != null) {
s1.push(head.right);
}
}
// 左 右 头
while (!s2.isEmpty()) {
System.out.print(s2.pop().value + " ");
}
}
System.out.println();
}
这里后序遍历其实跟前序遍历是一样的,前序遍历是根,左,右。后序是根,右,左。
其实只需要再加一个栈来区别他是左边的还是右边的就好。
中序遍历方式:
public static void in(Node cur) {
System.out.print("in-order: ");
if (cur != null) {
Stack<Node> stack = new Stack<Node>();
while (!stack.isEmpty() || cur != null) {
if (cur != null) {
// head整条左边树进栈,除去空的情况
stack.push(cur);
cur = cur.left;
} else {
// 右节点为空的时候弹出打印
// 从栈中弹出节点打印,这个节点的右孩子为cur
cur = stack.pop();
System.out.print(cur.value + " ");
cur = cur.right;
}
}
}
System.out.println();
}
中序先将左树全部进栈,右节点为空的时候就弹出,在把当前节点给到他的左父节点。
后序遍历的话其实也可以用一个栈来实现:
// 一个栈实现
public static void pos2(Node h) {
System.out.print("pos-order: ");
if (h != null) {
Stack<Node> stack = new Stack<Node>();
stack.push(h);
Node c = null;
while (!stack.isEmpty()) {
c = stack.peek();
if (c.left != null && h != c.left && h != c.right) {
stack.push(c.left);
} else if (c.right != null && h != c.right) {
stack.push(c.right);
} else {
System.out.print(stack.pop().value + " ");
h = c;
}
}
}
System.out.println();
}
public static void main(String[] args) {
Node head = new Node(1);
head.left = new Node(2);
head.right = new Node(3);
head.left.left = new Node(4);
head.left.right = new Node(5);
head.right.left = new Node(6);
head.right.right = new Node(7);
pre(head);
System.out.println("========");
in(head);
System.out.println("========");
pos1(head);
System.out.println("========");
pos2(head);
System.out.println("========");
}

 菜鸟笔记
菜鸟笔记