一:基本原理
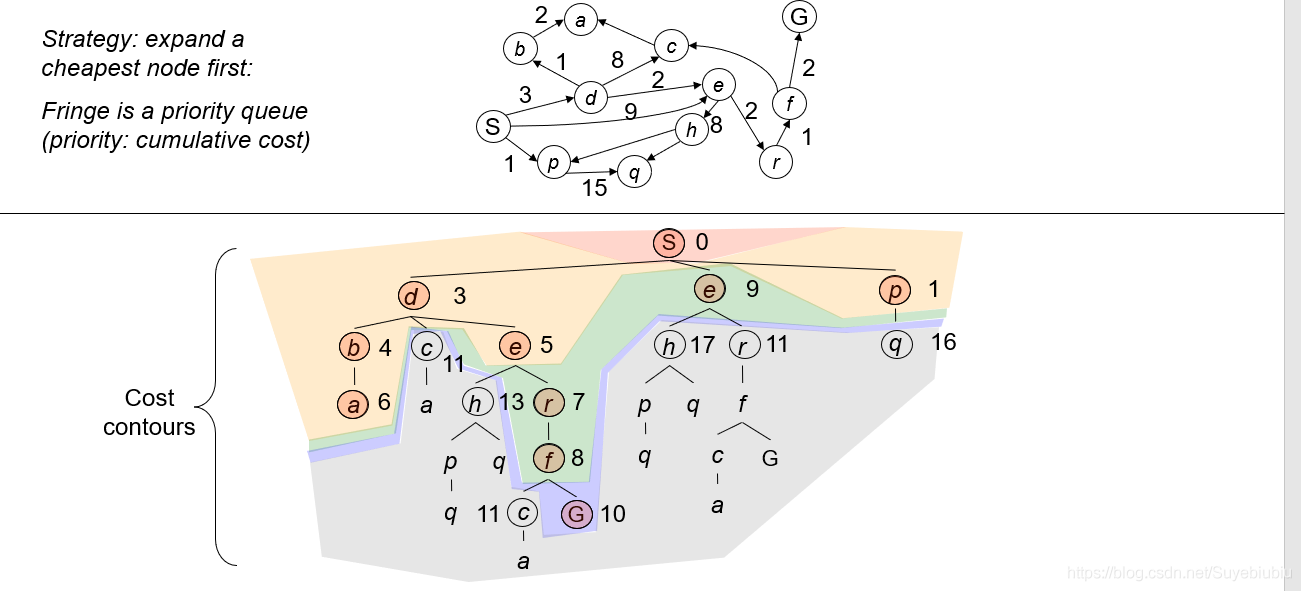
一致代价搜索是在广度优先搜索上进行扩展的,也被成为代价一致搜索,他的基本原理是:一致代价搜索总是扩展路径消耗最小的节点N。N点的路径消耗等于前一节点N-1的路径消耗加上N-1到N节点的路径消耗。
图的一致性代价搜索使用了优先级队列并在边缘中的状态发现更小代价的路径时引入的额外的检查。边缘的数据结构需要支持有效的成员校测,这样它就结合了优先级队列和哈希表的能力。
我们以前在高级人工智能第一篇讲无信息搜索的文章中(https://blog.csdn.net/Suyebiubiu/article/details/100738725),有一个例子是有名的罗马尼亚的旅行问题。我们这次可以尝试着用一致代价搜索方式进行解决这个问题。
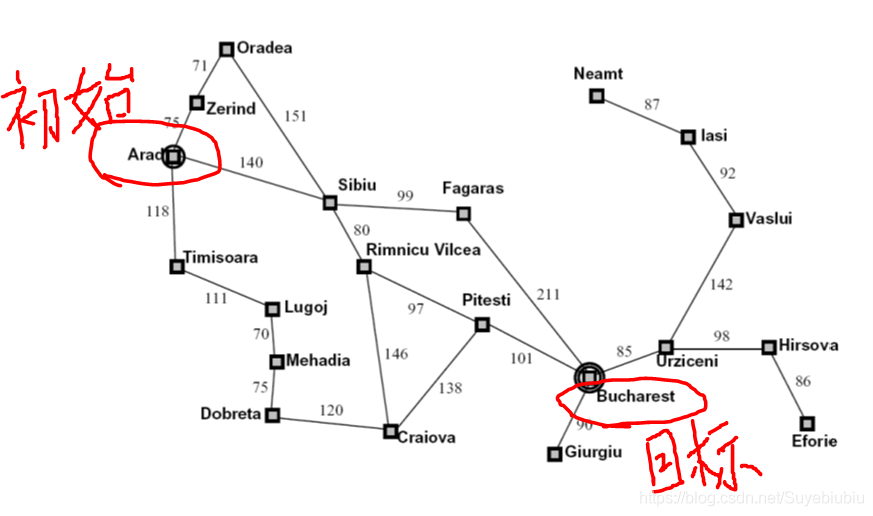
我们想要从Arad到达Bucharest,姑且认为是A和B两个位置,我们想要使用一致代价搜索方式
- 1.根据上图创建一个搜索树,以A为初始状态,B为目标状态
- 2.实现代价一致搜索的图搜索算法并记录搜索路径
二:算法实现流程
frontier:边缘。存储未扩展的节点。优先级队列,按路径消耗来排列
explored:探索集。存储的是状态
2.1 流程分析:
1.如果边缘为空,则返回失败。操作:EMPTY?(frontier)
2.否则从边缘中选择一个叶子节点。操作:POP(frontier)
3.目标测试:通过返回,否则将叶子节点的状态放在探索集
4.遍历叶子节点的所有动作
- 每个动作产生子节点
- 如果子节点的状态不在探索集或者边缘,则插入到边缘集合。操作:INSERT(child, frontier)
- 否则如果边缘集合中如果存在此状态且有更高的路径消耗,则用子节点替代边缘集合中的状态

A是起点,C是终点。
2.2 一致代价搜索算法执行:
- A放入frontier
- —第1次
- 从frontier中取出A(此时路径消耗最小)检测发现不是目标
- A放入explored
- 遍历A的子节点,D和B放入frontier
- —第2次
- 从frontier中取出D(此时路径消耗最小)检测发现不是目标
- D放入explored
- 遍历D的子节点,C放入frontier
- —第3次
- 从frontier中取出B(此时路径消耗最小)检测发现不是目标
- B放入explored
- 遍历B的子节点,E放入frontier
- —第4次
- 从frontier中取出E(此时路径消耗最小)检测发现不是目标
- E放入explored
- 遍历E的子节点,C准备放入frontier,发现此时frontier已有C,但路径消耗为8大于7,则替代frontier中的C
- —第5次
- 从frontier中取出C(此时路径消耗最小)检测发现是目标,成功
- 最优路径:A->B->E->C
从上例可以看出,一致代价搜索具有最优性,关键在于frontier中存储是按路径消耗顺序来排序的。
2.3 算法性能分析:
2.3.1:分析一致代价搜索的完备性、最优性、时间和空间复杂度

2.3.2:指出无信息搜索策略和有信息搜索策略的不同

2.3.3:分析一致代价搜索如何保证算法的最优性

三:源代码分析
import pandas as pd
from pandas import Series, DataFrame
# 城市信息:city1 city2 path_cost
_city_info = None
# 按照路径消耗进行排序的FIFO,低路径消耗在前面
_frontier_priority = []
# 节点数据结构
class Node:
def __init__(self, state, parent, action, path_cost):
self.state = state
self.parent = parent
self.action = action
self.path_cost = path_cost
def main():
global _city_info
import_city_info()
while True:
src_city = input('输入初始城市\n')
dst_city = input('输入目的城市\n')
# result = breadth_first_search(src_city, dst_city)
result = uniform_cost_search(src_city, dst_city)
if not result:
print('从城市: %s 到城市 %s 查找失败' % (src_city, dst_city))
else:
print('从城市: %s 到城市 %s 查找成功' % (src_city, dst_city))
path = []
while True:
path.append(result.state)
if result.parent is None:
break
result = result.parent
size = len(path)
for i in range(size):
if i < size - 1:
print('%s->' % path.pop(), end='')
else:
print(path.pop())
def import_city_info():
global _city_info
data = [{'city1': 'Oradea', 'city2': 'Zerind', 'path_cost': 71},
{'city1': 'Oradea', 'city2': 'Sibiu', 'path_cost': 151},
{'city1': 'Zerind', 'city2': 'Arad', 'path_cost': 75},
{'city1': 'Arad', 'city2': 'Sibiu', 'path_cost': 140},
{'city1': 'Arad', 'city2': 'Timisoara', 'path_cost': 118},
{'city1': 'Timisoara', 'city2': 'Lugoj', 'path_cost': 111},
{'city1': 'Lugoj', 'city2': 'Mehadia', 'path_cost': 70},
{'city1': 'Mehadia', 'city2': 'Drobeta', 'path_cost': 75},
{'city1': 'Drobeta', 'city2': 'Craiova', 'path_cost': 120},
{'city1': 'Sibiu', 'city2': 'Fagaras', 'path_cost': 99},
{'city1': 'Sibiu', 'city2': 'Rimnicu Vilcea', 'path_cost': 80},
{'city1': 'Rimnicu Vilcea', 'city2': 'Craiova', 'path_cost': 146},
{'city1': 'Rimnicu Vilcea', 'city2': 'Pitesti', 'path_cost': 97},
{'city1': 'Craiova', 'city2': 'Pitesti', 'path_cost': 138},
{'city1': 'Fagaras', 'city2': 'Bucharest', 'path_cost': 211},
{'city1': 'Pitesti', 'city2': 'Bucharest', 'path_cost': 101},
{'city1': 'Bucharest', 'city2': 'Giurgiu', 'path_cost': 90},
{'city1': 'Bucharest', 'city2': 'Urziceni', 'path_cost': 85},
{'city1': 'Urziceni', 'city2': 'Vaslui', 'path_cost': 142},
{'city1': 'Urziceni', 'city2': 'Hirsova', 'path_cost': 98},
{'city1': 'Neamt', 'city2': 'Iasi', 'path_cost': 87},
{'city1': 'Iasi', 'city2': 'Vaslui', 'path_cost': 92},
{'city1': 'Hirsova', 'city2': 'Eforie', 'path_cost': 86}]
_city_info = DataFrame(data, columns=['city1', 'city2', 'path_cost'])
# print(_city_info)
def breadth_first_search(src_state, dst_state):
global _city_info
node = Node(src_state, None, None, 0)
# 目标测试
if node.state == dst_state:
return node
frontier = [node]
explored = []
while True:
if len(frontier) == 0:
return False
node = frontier.pop(0)
explored.append(node.state)
if node.parent is not None:
print('处理城市节点:%s\t父节点:%s\t路径损失为:%d' % (node.state, node.parent.state, node.path_cost))
else:
print('处理城市节点:%s\t父节点:%s\t路径损失为:%d' % (node.state, None, node.path_cost))
# 遍历子节点
for i in range(len(_city_info)):
dst_city = ''
if _city_info['city1'][i] == node.state:
dst_city = _city_info['city2'][i]
elif _city_info['city2'][i] == node.state:
dst_city = _city_info['city1'][i]
if dst_city == '':
continue
child = Node(dst_city, node, 'go', node.path_cost + _city_info['path_cost'][i])
print('\t孩子节点:%s 路径损失为%d' % (child.state, child.path_cost))
if child.state not in explored and not is_node_in_frontier(frontier, child):
# 目标测试
if child.state == dst_state:
print('\t\t 这个孩子节点就是目的城市')
return child
frontier.append(child)
print('\t\t 添加孩子节点到这个孩子')
def is_node_in_frontier(frontier, node):
for x in frontier:
if node.state == x.state:
return True
return False
def uniform_cost_search(src_state, dst_state):
global _city_info, _frontier_priority
node = Node(src_state, None, None, 0)
frontier_priority_add(node)
explored = []
while True:
if len(_frontier_priority) == 0:
return False
node = _frontier_priority.pop(0)
if node.parent is not None:
print('处理城市节点:%s\t父节点:%s\t路径损失为:%d' % (node.state, node.parent.state, node.path_cost))
else:
print('处理城市节点:%s\t父节点:%s\t路径损失为:%d' % (node.state, None, node.path_cost))
# 目标测试
if node.state == dst_state:
print('\t 目的地已经找到了')
return node
explored.append(node.state)
# 遍历子节点
for i in range(len(_city_info)):
dst_city = ''
if _city_info['city1'][i] == node.state:
dst_city = _city_info['city2'][i]
elif _city_info['city2'][i] == node.state:
dst_city = _city_info['city1'][i]
if dst_city == '':
continue
child = Node(dst_city, node, 'go', node.path_cost + _city_info['path_cost'][i])
print('\t孩子节点:%s 路径损失为:%d' % (child.state, child.path_cost))
if child.state not in explored and not is_node_in_frontier(_frontier_priority, child):
frontier_priority_add(child)
print('\t\t 添加孩子到优先队列')
elif is_node_in_frontier(_frontier_priority, child):
# 替代为路径消耗少的节点
frontier_priority_replace_by_priority(child)
def frontier_priority_add(node):
"""
:param Node node:
:return:
"""
global _frontier_priority
size = len(_frontier_priority)
for i in range(size):
if node.path_cost < _frontier_priority[i].path_cost:
_frontier_priority.insert(i, node)
return
_frontier_priority.append(node)
def frontier_priority_replace_by_priority(node):
"""
:param Node node:
:return:
"""
global _frontier_priority
size = len(_frontier_priority)
for i in range(size):
if _frontier_priority[i].state == node.state and _frontier_priority[i].path_cost > node.path_cost:
print('\t\t 替换状态: %s 旧的损失:%d 新的损失:%d' % (node.state, _frontier_priority[i].path_cost,
node.path_cost))
_frontier_priority[i] = node
return
if __name__ == '__main__':
main()
四:运行结果

输入初始城市
Arad
输入目的城市
Bucharest
处理城市节点:Arad 父节点:None 路径损失为:0
孩子节点:Zerind 路径损失为:75
添加孩子到优先队列
孩子节点:Sibiu 路径损失为:140
添加孩子到优先队列
孩子节点:Timisoara 路径损失为:118
添加孩子到优先队列
处理城市节点:Zerind 父节点:Arad 路径损失为:75
孩子节点:Oradea 路径损失为:146
添加孩子到优先队列
孩子节点:Arad 路径损失为:150
处理城市节点:Timisoara 父节点:Arad 路径损失为:118
孩子节点:Arad 路径损失为:236
孩子节点:Lugoj 路径损失为:229
添加孩子到优先队列
处理城市节点:Sibiu 父节点:Arad 路径损失为:140
孩子节点:Oradea 路径损失为:291
孩子节点:Arad 路径损失为:280
孩子节点:Fagaras 路径损失为:239
添加孩子到优先队列
孩子节点:Rimnicu Vilcea 路径损失为:220
添加孩子到优先队列
处理城市节点:Oradea 父节点:Zerind 路径损失为:146
孩子节点:Zerind 路径损失为:217
孩子节点:Sibiu 路径损失为:297
处理城市节点:Rimnicu Vilcea 父节点:Sibiu 路径损失为:220
孩子节点:Sibiu 路径损失为:300
孩子节点:Craiova 路径损失为:366
添加孩子到优先队列
孩子节点:Pitesti 路径损失为:317
添加孩子到优先队列
处理城市节点:Lugoj 父节点:Timisoara 路径损失为:229
孩子节点:Timisoara 路径损失为:340
孩子节点:Mehadia 路径损失为:299
添加孩子到优先队列
处理城市节点:Fagaras 父节点:Sibiu 路径损失为:239
孩子节点:Sibiu 路径损失为:338
孩子节点:Bucharest 路径损失为:450
添加孩子到优先队列
处理城市节点:Mehadia 父节点:Lugoj 路径损失为:299
孩子节点:Lugoj 路径损失为:369
孩子节点:Drobeta 路径损失为:374
添加孩子到优先队列
处理城市节点:Pitesti 父节点:Rimnicu Vilcea 路径损失为:317
孩子节点:Rimnicu Vilcea 路径损失为:414
孩子节点:Craiova 路径损失为:455
孩子节点:Bucharest 路径损失为:418
替换状态: Bucharest 旧的损失:450 新的损失:418
处理城市节点:Craiova 父节点:Rimnicu Vilcea 路径损失为:366
孩子节点:Drobeta 路径损失为:486
孩子节点:Rimnicu Vilcea 路径损失为:512
孩子节点:Pitesti 路径损失为:504
处理城市节点:Drobeta 父节点:Mehadia 路径损失为:374
孩子节点:Mehadia 路径损失为:449
孩子节点:Craiova 路径损失为:494
处理城市节点:Bucharest 父节点:Pitesti 路径损失为:418
目的地已经找到了
从城市: Arad 到城市 Bucharest 查找成功
Arad->Sibiu->Rimnicu Vilcea->Pitesti->Bucharest五:结果说明


 菜鸟笔记
菜鸟笔记